I.14.2
PREVIOUS INTERPRETATIONS
CONTRADICTORY TITLES NOT PART
OF THE ORIGINAL SCHEME
Two of the earlier students of the Plan, Hugo Graf[317]
and
August Hardegger[318]
proposed to solve these inconsistencies
with the assumption that the explanatory titles were not
part of the original textual annotations of the Plan but were
inserted at a later time, presumably when the plan was
subjected to a final revision before the actual construction
of the church by Abbot Gozbert in 830. Bischoff's palaeographical
analysis of the inscriptions has disproved this view
by establishing that the titles that list the dimensions of
the Church were written by the same hand that wrote the
letter of transmittal, whose writer refers to himself explicitly
as the author of the Plan.[319]
The measurements, for this
reason, cannot be ascribed to a revision undertaken by
Abbot Gozbert or any of his builders. Their inconsistency
with the drawing is an intrinsic feature of the Plan itself.
THE TITLES NOT THE DRAWING REFLECT
THE INTENT OF THE ORIGINAL SCHEME
In attempting to explain this disturbing incongruity
three further theories have evolved. One group of students
of the Plan proposed that the linear layout of the Church
was only a schematic concept and that the true intent of the
draftsman was revealed not in the drawing, but in the
accompanying explanatory titles. The main proponents of
this view are Georg Dehio,[320]
Joseph Hecht,[321]
Wilhelm
Pinder,[322]
Hans Reinhardt,[323]
and Wolfgang Schöne.[324]
All
made an attempt to reconstruct what they believed to be
the author's "true intentions" by modifying the plan of the
Church in the light of the measurements listed in its
explanatory legends.[325]
THE DRAWING NOT THE TITLES
SHOULD BE TRUSTED
A second group of scholars, comprised of Wilhelm
Effman,[326]
Friedrich Ostendorf,[327]
Ernst Gall,[328]
Edgar
Lehman,[329]
Otto Doppelfeld,[330]
and Wilhelm Rave[331]
chose
to give credence to the drawing rather than to the explanatory

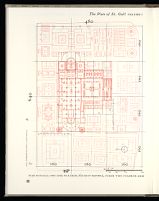
[ILLUSTRATION]
PLAN OF ST. GALL. MONKS' DORMITORY
A. Facsimile reproduction of the red drawing of the Plan (see caption, page 13, vol. III)
B. Same, with 2½-foot module superimposed
C. Probable scheme by which the layout shown in A was constructed
After the area analyzed in Fig. 59, the
Monks' Dormitory embodies the next most
obvious proof that in designing the Plan, the
maker used an accurately graduated scale.
The basic unit of this scale, the 2½-foot
measure, the designer obtained by halving four
times in succession the width he assigned to
the nave of the Church, its transept, and all
the basic claustral structures (see pp. 89-90
and Ernest Born's diagrams and captions,
pp. 92-93).
A 2½-foot module was a felicitous
size for the basic unit of measurement
applying to a settlement the size of the
monastery of the Plan. It was large enough
to account for critical space (seating,
sleeping) and small enough to obviate the
need to draw in excessive detail, and thus to
cloud the view of the community's buildings.
With a practical understanding, the maker
of the Plan rounded up his dimensions to the
next higher—never the lower—module:
furnishings or features that might, when
installed, lay in size between one and another
module, were drawn to the larger size.
This choice was deliberate. The beds of the
Monks' Dormitory, and all other places
where beds are depicted on the Plan (Abbot's
House, House for Distinguished Guests,
Dormitory for Visiting Monks), are examples
of it. All these beds are assigned a width of
one module and a length of three. One module
2½ feet (30 inches) might be considered
adequate for the width of a monk's cot,
but three modules totalling 7½ feet seems
overly long. However, the space of two
modules, 5 feet, would surely have been too
short for a grown man. The longer increment
allowed the designer to indicate just how
many were expected to sleep in a space the
size of the Dormitory; to suggest a possible
bed arrangement while permitting enough
more space to accommodate furnishings; and,
by accumulation of "extra" measure,
ultimately to account for space required by
such constructional features as wall thick-
nesses and staircases, nowhere specifically
indicated on the Plan. Such issues would have
been resolved as a function of supervision
in actual construction, decisions delegated
to an experienced artisan who not only could
understand and interpret the Plan and its
maker's intentions, but who also knew how
to deal with practicalities of building a
wing to house 76 men. More discussion of
these issues is offered, pp. 112-13, and II,
225ff.
60.
titles. To them the Church with the thickness of its
walls reconstructed, would have looked as it is shown in
figure 56 (a proposal made by Ostendorf).
[332]
Doppelfeld, the most articulate exponent of this group,
has proposed that the inconsistencies between the drawing
and the measurements given in the explanatory titles can
be easily resolved if one were to assume that the scribe who
wrote these legends converted the figure 300 (in Latin,
CCC) into 200 (in Latin, CC) by inadvertently dropping
one of the C's; and that he committed a second error by
confusing a d with an s and thus inadvertently converting
the crucial word bis denos ("twice ten," equaling twenty) of
the intercolumniary legend of the arcades of the nave of
the church into bis senos ("twice six," equaling twelve). If
these errors of the copyist are corrected, Doppelfeld concluded,
all the discrepancies between the drawing and its
explanatory titles would disappear, and the text and drawing
would endorse one another.[333]
Doppelfeld had another reason for believing in the trustworthiness
of the drawing: his own excavations beneath the
pavement of Cologne Cathedral which had brought to light
the foundations of a Carolingian monastery church whose
dimensions were virtually identical to those of the Church
of St. Gall.[334]
THE INCONSISTENCIES NOT PART OF THE
ORIGINAL CONCEPT BUT A CORRECTIVE MEASURE
Doppelfeld's argument was persuasive, and it was based
on a hypothesis subsequently proven to be correct, namely,
that the Plan of St. Gall is not an original but a copy.[335]
Yet
even before this fact was established, Doppelfeld's view
was challenged by Walter Boeckelmann.[336]
The incompatibility
between the drawing and the explanatory titles,
Boeckelmann contended, was not the product of an erring
scribe, but the reflection of a conflict that had arisen at the
council of Aachen, held in 816,[337]
between the bold dimensional
thinking of the old ecclesiastical leaders who had
shaped the policy of the church under Charlemagne and
the constrictive views of the leaders of the reform party
who controlled the church under Louis the Pious. A plan
worked out by the "old guard" had come under the
criticism of the reform party. The dimensions listed in the
explanatory titles were not meant to explain the drawing,
but to correct it. And since the proponents of these corrective
measures did not take it upon themselves to revise the
drawing in the suggested sense, "the disagreement was not
solved in the Plan, the conflict remaining preserved."
Boeckelmann's view, in my opinion, is correct. It reconciles
more of the conflicting traits of the Plan than any of
the previous hypotheses. More recent investigations have
shown that there indeed existed a serious ideological split
at the synods of Aachen between an old conservative group
of churchmen and the leaders of the reform party, which
affected other aspects of the Plan.[338]
CONFLICTING VIEWS ON SCALE OF THE PLAN
But Boeckelmann's theory was challenged, in turn, in
1965 by Adolf Reinle,[339]
who came forth with a new interpretation
of the textual incongruities of the Plan that
departed radically from all views previously expressed on
this subject. The meaning of the axial title of the Church, so
Reinle contended, is not as is generally assumed,
FROM EAST TO WEST
THE LENGTH IS 200 FEET
but rather,
THIS PLAN IS DRAWN AT THE
SCALE OF 1:200
Reinle arrived at this interpretation in the following
manner:
1. PED̄, he maintained, must not be transcribed as
PEDUM (genitive plural of pes = "foot"), but as PEDA or
PEDIA (imperative form of the verb pedare or pediare = "to
measure in feet").[340]
2. LONGĪT̄. must not be read as LONGITUDO (nominative
of the noun longitudo = "length"), but as LONGITUDINE
(ablative form of the noun longitudo = "in length").[341]
3. .CC. is not the simple cardinal figure ducentum =
"two hundred," but must be interpreted as a multiplicative
term, in the sense of ducenties = "two hundred times."
Reinle, accordingly, transcribes the title:
AB ORIENTE IN OCCIDENTEM
LONGITUDINE PEDA DUCENTIES
and purports this to mean
FROM EAST TO WEST, IN LENGTH,
MEASURE TWO HUNDRED TIMES,
or
THIS PLAN IS
DRAWN AT THE SCALE OF 1:200.[342]
This interpretation is untenable on two counts: first, it is
based on an improper textual exegesis; and second, it
ascribes to the ninth century a method of defining architectural
scale relationships that does not antedate the French
Revolution.[343]
IMPROPER TEXTUAL EXEGESIS
It is apparent that Reinle's interpretation of the axial title
of the Church has been undertaken without reference to the
Latinity of the other titles of the Plan and their system of
graphical abbreviations. The Plan, as we have seen,[344]
is
furnished with some 340 separate entries of varying length,
the majority in prose, the remainder in verse. The prose is
lucid and not susceptible to misinterpretation at any point.
The verses are often flowery in style, but their syntax and
sense are always clear. There is nothing equivocal about the
distich that defines the interstices between the columns of
the nave arcades (No. 4) or the hexameter that defines the
interstices between the piers of the western Paradise (No.
5). And there is nothing equivocal about the style or syntax
of any of the other titles of the Plan. It is inconceivable
within the total context of these legends that the drafter of
these texts would have framed one of the most crucial lines
of his commentary in so sloppy a manner as to mislead
some seven generations of Latinists into interpreting as a
simple designation of length what he meant to be a ratio of
scale.
If PED̄ had been meant to stand for PEDA, the scribe would
have found himself compelled to make this clear by spelling
the word out—as he had done in title 4 (metire) and title 5
(moderare) where this form is used—in view of the fact that
PED̄ is the traditional abbreviation for PEDUM. By the same
token, he would have had to make it clear that LONGĪT̄
stood for LONGITUDINE, rather than allowing it to be read as
LONGITUDO. And if the capital letters CC were meant to
convey the meaning "two hundred times," rather than the
figure 200, the scribe would have had to make this clear,
since such a use of the letters would have differed distinctly
from their traditional usage. The need for this clarification
would have been the more pressing because clearly all of
the other dimensional titles on the Plan are designations of
simple linear length. No reader of the Plan can fail to notice
that the syntax of the longitudinal title of the Church (No.
1) and the two titles that describe the width of the nave and
the aisles (No. 2 and 3) is identical. Each consists of a
subject (LONGIT[UDO], Latitudo, Latitudo), a prepositional
phrase (AB ORIENTE IN OCCIDENTE[M], interioris templi,
utriusque porticus), and a predicate phrase (PED[UM] .CC.,
pedu[m] xl, pedum xx). The verb est is missing, but is
implicit in the text, and it is, therefore, entirely proper to
translate these respective passages (1, 2, 3, above) as:
FROM EAST TO WEST
THE LENGTH IS 200 FEET
THE WIDTH OF THE NAVE IS 40 FEET
THE WIDTH OF EACH AISLE IS 20 FEET
What was it that induced Reinle to engage in such arbitrary
textual exegesis? This question takes us to our second
main objection:
ANACHRONISM IN MENSURATION
Reinle believes he has discovered that the Plan of St. Gall
was drawn at a scale of 1:200.[345]
He is not the first to
advance this view. Wilhelm Rave had expressed himself
along similar lines in 1956,[346]
and Emil Reisser likewise, in a
study published posthumously in 1960.[347]
The Plan is, indeed, drawn to a scale that comes close to
what we would define today as a ratio of 1:200. But it is one
thing to observe that the Plan was drawn at a scale that
corresponds or comes close to the ratio of 1:200; it is quite
another to claim that it was actually drawn at that scale. In
proposing this view, Reinle is caught in an anachronism.
The concept 1:200 is not a medieval concept and does not
make sense within the medieval system of mensuration. If a
modern architectural drawing is said to be laid out at a
scale of 1:200, this means that one unit on the drawing
corresponds to 200 identical units on the ground. The base
of this ratio is decimal. A medieval architect could not have
expressed himself in these terms, since the two basic units
of measurement with which he worked, the foot and the
inch, were internally divided not into tenths, but into
twelfths and sixteenths (a system that still persists in
England and the larger Anglo-Saxon world) or into
twelfths and twelfths (the pied royal de France, which was
used in France until the introduction of the metric system).[348]
The foot and its primary subdivision, the inch, were
derived from the human body.[349]
Twelve thumb-breadths
of a fully grown man equal the length of his foot (fig. 57).
This is the raison d'être for the twelve units of the English
foot. The French word pouce, the Old French poulcée, the
Latin pollex—all meaning "thumb"—reflect the history of
the genesis of this measure. Like the English foot, the
Latin foot consisted of twelve units[350]
"Inch," Anglo-Saxon
ynce, comes from Latin uncia = "a twelfth"; and
the duodecimal graduation of the Roman foot is reflected
in the series: uncia = 1/12;
| sextans |
= 2/12 or ⅙ |
| quadrans |
= 3/12 or ¼ |
| triens |
= 4/12 or ⅓ |
| quincunx |
= 5/12 |
| semipes |
= 6/12 or ½ |
| septunx |
= 7/12 |
| bes |
= 8/12 or ⅔ |
| dodrans |
= 9/12 or ¾ |
| dextans |
= 10/12 or ⅙ |
| deunx |
= 11/12 |
[ILLUSTRATION]
62. PLAN OF ST GALL: SHOWING 40 FOOT MODULE SUPERIMPOSED UPON
THE ENTIRE SITE OF THE MONASTERY
The human body does not offer reliable guidance for
divisions smaller than the breadth of a thumb. These
smaller units could only be obtained by instrumental
operations, and the simplest, easiest, and for that reason,
probably the oldest, way of graduating a distance into a
sequence of consistently decreasing smaller units is the
method of continuous halving—a procedure by means of
which a whole is reduced to a half, a half to a quarter, a
quarter to an eighth, and eighth to a sixteenth (fig. 58).[351]
This is the procedure that created the sixteen graduations
of the English inch.[352]
We know nothing about the internal divisions of the
Carolingian inch, but whether it was graduated into twelfths
or into sixteenths, this much is certain: there was no
common decimal denominator between a Carolingian inch
and a Carolingian foot that could be expressed in the ratio
1:200.
The modern metric scale is based on a comparison of
parts of like nature, all of which can be understood either
as fractions or as multiples of ten. The medieval scale has
no such common unit of reference. It is a combination of a
variety of different forms of graduation (sedecimal, duo-
1. Corporibus. Scilicet non solum de temporibus.
2. Miliarium. Id sunt mille passus. Legua enim ·I· D· passus.
3. Stadium. Id est ·CXXV· passus. Stadium octava pars miliarii est.
4. Iugerum. ·XLVIII· passus. Iugerum est quod possunt duo boves in una
die arare, id est iornalis.
5. Perticam. Decem pedes . . .
6. Dimidium. Id est medietas.
7. Semis. Scilicet non solum appellatur medietas librae semis, sed etiam
medietas cubiti et ideo dixit in corporibus.
8. Semis. Scilicet ubi semis ponitur, non ponitur et coniunctio.
9. Semissem. Id est dimidium. Accusativus a semis.
"Bede had asserted that the traditional measures had to be adapted to
duodecimals. But the Metz glossator, in introducing these definitions,
gratuitously introduced other schemes of fractions. Granted (2) that a
mile is a thousand paces, a league is 3/2 thousand. A stade (3) is 125
paces, an eighth of a mile. An acre (4) is 48 paces, a rod (5) ten paces. At
this stage of the pattern, medietas (6), the mid-point, becomes a congenial
concept for one half, not only for the semi-pound (7) but for the semicubit,
`and therefore it is used in measuring bodies,' a usage justified
for Bede by no lesser an authority than Moses (Exodus xxv.10) who used
dimidium and semissem in the same sentence interchangably. Hence it
seems that the Metz glossator found it easy, with his mind centered on
the building measurements of Noah's and Moses' arks, to introduce a
scheme of fractions quite at odds with the duodecimalism he was teaching
as the determining ratio of weights and measures."
[ILLUSTRATION]
63. PLAN OF ST. GALL: ONE LINE OF A GRID, 160 FOOT MODULE, FIXED THE CHURCH AXIS
decimal, and decimal), whose relation to one another cannot
be expressed in the terms of a decimal sequence.
It would be correct to say that the Plan of St. Gall is
drawn to a scale in which one sixteenth of a Carolingian
inch on the drawing corresponds to one Carolingian foot
on the ground. To convert this scale into a relationship in
which the ratio is expressed in the form of like units
requires that the base value of one sixteenth of an inch be
multiplied first by 16 (the sixteen parts of the inch) and then
by 12 (the twelve parts of the foot): 16 × 12 = 192,[353]
the
number of sixteenths of an inch in a foot. The ratio 1:192
is not far from the ratio 1:200, but it is not identical with it
and should, under no circumstances, be confused with it.[354]
In medieval mensuration the scale relationship 1:200 not
only did not exist, it would have been meaningless.[355]
This
fact by itself precludes that the axial title of the Church
could have meant what Reinle purports it to mean, and
thus we are taken back to Boeckelmann's interpretation as
the most reasonable explanation of the dimensional incongruities
of the Plan.
EARLY EXPRESSION OF THE VIEW THAT
THE PLAN WAS DRAWN TO A CONSISTENT SCALE
In contrast to those who held that the Plan of St. Gall
was purely a schematic rendering, Boeckelmann believed
that the Plan was drawn to a definite scale and that the key
to this scale was to be found in the 40 feet that the draftsman
ascribed to the width of the nave of the Church. He
observed that values consistent with this scale can be recognized
in the dimensions of many other areas of the Plan.
The Cloister Yard, for example, if measured in the light of
the 40-foot width of the nave, forms a square of 100 feet;
the rectangular area in its center, a square of 20 feet.[356]
Boeckelmann was not the first to make this observation.
As early as 1938, Fritz Viktor Arens had drawn attention
to the fact that many of the dimensions of the Plan of St.
Gall were based upon a decimal system consistent with the
40-foot width of the nave of the Church.[357]
He also observed
another important fact, that if one attempted to
redraw the Plan of St. Gall in the light of the measurements
given for the length of the Church (200 feet), the Cloister
and all service structures of the Plan would be reduced to a
size in which they could no longer perform their designated
functions.[358]
It was the most stringent argument in favor of
the assumption that if any of the measurements given in
the explanatory titles of the Plan reflect the original scale,
it is the 40-foot figure listed for the width of the nave, and
not the 200-foot figure listed for the length of the Church.
Arens' and Boeckelmann's observations were fundamental.
Yet neither Arens nor Boeckelmann realized their
full significance. Their failure to do so was probably caused
by their awareness that, whereas the dimensions of many of
the larger installations of the Plan can clearly be interpreted
as multiples of ten, many others—and in particular the
majority of all the smaller dimensional values of the Plan—
are inexplicable in the context of a decimal scale.