The Plan of St. Gall a study of the architecture & economy of & life in a paradigmatic Carolingian monastery |
| I. |
| I. |
| I. 1. |
| I.1.1. |
| I.1.2. |
| I.1.3. |
| I.1.4. |
| I.1.5. |
| I.1.6. |
| I.1.7. |
| I. 2. |
| I.2.1. |
| I. 3. |
| I.3.1. |
| I.3.2. |
| I.3.3. |
| I. 4. |
| I.4.1. |
| I.4.2. |
| I. 5. |
| I.5.1. |
| I.5.2. |
| I.5.3. |
| I. 6. |
| I.6.1. |
| I. 7. |
| I.7.1. |
| I.7.2. |
| I.7.3. |
| I.7.4. |
| I. 8. |
| I. 9. |
| I.9.1. |
| I. 10. |
| I.10.1. |
| I.10.2. |
| I. 11. |
| I.11.1. |
| I.11.2. |
| I. 12. |
| I.12.1. |
| I.12.2. |
| I.12.3. |
| I.12.4. |
| I.12.5. |
| I.12.6. |
| I.12.7. |
| I. 13. |
| I.13.1. |
| I.13.2. |
| I.13.3. |
| I.13.4. |
| I.13.5. |
| I.13.6. |
| I.13.7. |
| I.13.8. |
| I. 14. | I. 14 |
| I.14.1. |
| I.14.2. |
| I.14.3. |
| I.14.4. |
| I.14.5. |
| I.14.6. |
| I.14.7. |
| I.14.8. |
| I.14.9. |
| I. 15. |
| I.15.1. |
| I. 16. |
| I. 17. |
| II. |
| II. 1. |
| II.1.1. |
| II.1.2. |
| II.1.3. |
| II.1.4. |
| II.1.5. |
| II.1.6. |
| II.1.7. |
| II.1.8. |
| II.1.9. |
| II.1.10. |
| II.1.11. |
| II.1.12. |
| II.1.13. |
| II. 2. |
| II.2.1. |
| II.2.2. |
| II. 3. |
| II.3.1. |
| II.3.2. |
| II.3.3. |
| II.3.4. |
| II.3.5. |
| II.3.6. |
| II.3.7. |
| II.3.8. |
| II.3.9. |
| II.3.10. |
| III. |
| III. 1. |
| III.1.1. |
| III.1.2. |
| III.1.3. |
| III.1.4. |
| III.1.5. |
| III.1.6. |
| III.1.7. |
| III.1.8. |
| III.1.9. |
| III.1.30. |
| III.1.11. |
| III. 2. |
| III.2.1. |
| III.2.2. |
| III.2.3. |
| III.2.4. |
| III.2.5. |
| III.2.6. |
| III.2.7. |
| III.2.8. |
| III. 3. |
| III.3.1. |
| III.3.2. |
| III.3.3. |
| III.3.4. |
| III.3.5. |
| IV. |
| IV. 1. |
| IV.1.1. |
| IV.1.2. |
| IV.1.3. |
| IV.1.4. |
| IV.1.5. |
| IV.1.6. |
| IV.1.7. |
| IV.1.8. |
| IV.1.9. |
| IV.1.10. |
| IV.1.11. |
| IV.1.12. |
| IV. 2. |
| IV.2.1. |
| IV.2.2. |
| IV.2.3. |
| IV. 3. |
| IV.3.1. |
| IV. 4. |
| IV.4.1. |
| IV.4.2. |
| IV. 5. |
| IV.5.1. |
| IV. 6. |
| IV.6.1. |
| IV. 7. |
| IV.7.1. |
| IV.7.2. |
| IV.7.3. |
| IV.7.4. |
| IV.7.5. |
| IV.7.6. |
| IV.7.7. |
| The Plan of St. Gall | ||

I. 14
SCALE & CONSTRUCTION
METHODS USED IN DESIGNING
THE PLAN
I.14.1
INCONSISTENCIES BETWEEN THE
DRAWING AND THE
EXPLANATORY TITLES
In 1848 Robert Willis first expressed the view that the Plan
of St. Gall was not drawn to scale and should be considered
merely as a diagrammatic scheme.[314]
Since then the question
of its measurements and construction method has become
the subject of a perplexing controversy. Although in the
course of this dispute practically every leading architectural
historian of the Middle Ages has had his say, no unanimity
has yet been reached in this matter.[315]
The controversy was caused by the fact that the dimensions
given in the explanatory titles of the Church (the only
place on the Plan where dimensions are listed) could not be
brought into agreement with the manner in which the
building is drawn. The titles that contain these dimensions
are written by the main scribe,[316]
four in the small and finely
articulated minuscule in which most of the other legends of
this scribe are written, and one in a widely spaced capitalis
rustica. They are (fig. 55):
1. In the longitudinal axis of the Church, written in capitalis rustica, in groups of two and three letters, so as to extend
the entire length of the Church:
AB ORI EN TE IN OC CI DEN Tē LON GĪT̄. PED̄ .CC.
traditionally transcribed as:
AB ORIENTE IN OCCIDENTE[M] LONGIT[UDO] PED[UM] CC.
and accordingly translated:
FROM EAST TO WEST THE LENGTH [IS] 200 FEET.
2. In the nave, written crosswise, midway between the altar of the Holy Cross and the ambo:
Latitudo interioris tēp̄li pedū xl
The width of the nave of the church [is] 40 feet.
3. In the aisles, in line with the preceding title:
| Latitudo utriusque porticus | pedum xx |
| The width of each aisle | [is] 20 feet |
4. Between the interstices of the columns of the nave arcades the distich:
| Bis senos metire pedes interque columnas | [southern row] |
| Ordine quas isto constituisse decet | [northern row] |
Measure twice six feet between the columns
To have them arranged in this way is suitable.
5. In the interstices of the piers of the western Paradise the hexameter:
Has interque pedes denos moderare columnas
Between these columns measure ten feet.

59. PLAN OF ST. GALL. MONASTERY CHURCH DETAIL, FACSIMILE RED PRINT
The south transept arm of the Monastery Church (A) is shown in original size (scale 1:192).
The superimposition of lines at 2½ foot intervals running north-south (B) and east-west (C) demonstrate that internal area divisions are
calculated as multiples of a 2½-foot module. The complete 2½-foot modular grid (D) forms a conceptual prime condition for laying out all
values smaller or larger than 40 feet.

Many other students of the Plan have observed that a
conflict exists between the figures defining the width of the
Church and those which are given for its length. If a scale
is constructed on the basis of the 40-foot width of the nave
and applied to the length of the Church, the over-all
dimensions of the latter would come not to 200 feet (as is
stipulated in No. 1), but to 300 feet; and if the same 40-foot
scale were applied to the interstices of the two great
columnar orders, the axial distance from the column to
column would not amount to 12 feet (as stipulated in No.
4), but to 20 feet, since the drawing shows this span as
being exactly one-half the width of the nave. How is this
conflict to be resolved?
Willis, 1848, 89: "The plan has evidently no pretension to have been
laid down to scale." The view was reiterated by A. Campion in a French
translation of Willis' article, published in Bulletin Monumental, XXXIV
1868, 361-406, and was inherited from there by Henry Leclercq: "Le
dessinateur n'a aucun souci de mettre à l'échelle . . . le plan doit être
considéré comme un simple diagramme" (in Cabrol-Leclercq, VI:1,
1924, col. 88).
Even as late as 1937 Reinhardt remarked: "Comme le dessin de l'église,
celui des autres constructions ne peut être pris a l'échelle. Le dessin est
purement schematique" (Reinhardt, 1937, 277).
A systematic study to settle this controversy could not be undertaken
before the publication in 1952 of the facsimile color print, which made the
Plan accessible to analysis by compass and rule, a task impossible to
undertake previously because of the risk of damage to the original.
I.14.2
PREVIOUS INTERPRETATIONS
CONTRADICTORY TITLES NOT PART
OF THE ORIGINAL SCHEME
Two of the earlier students of the Plan, Hugo Graf[317]
and
August Hardegger[318]
proposed to solve these inconsistencies
with the assumption that the explanatory titles were not
part of the original textual annotations of the Plan but were
inserted at a later time, presumably when the plan was
subjected to a final revision before the actual construction
of the church by Abbot Gozbert in 830. Bischoff's palaeographical
analysis of the inscriptions has disproved this view
by establishing that the titles that list the dimensions of
the Church were written by the same hand that wrote the
letter of transmittal, whose writer refers to himself explicitly
as the author of the Plan.[319]
The measurements, for this
reason, cannot be ascribed to a revision undertaken by
Abbot Gozbert or any of his builders. Their inconsistency
with the drawing is an intrinsic feature of the Plan itself.
THE TITLES NOT THE DRAWING REFLECT
THE INTENT OF THE ORIGINAL SCHEME
In attempting to explain this disturbing incongruity
three further theories have evolved. One group of students
of the Plan proposed that the linear layout of the Church
was only a schematic concept and that the true intent of the
draftsman was revealed not in the drawing, but in the
accompanying explanatory titles. The main proponents of
this view are Georg Dehio,[320]
Joseph Hecht,[321]
Wilhelm
Pinder,[322]
Hans Reinhardt,[323]
and Wolfgang Schöne.[324]
All
made an attempt to reconstruct what they believed to be
the author's "true intentions" by modifying the plan of the
Church in the light of the measurements listed in its
explanatory legends.[325]
The first modified drawing of the Plan was published by Dehio and
von Bezold, Plates I, 1887, pl. 42 fig. 2. The same drawing is reproduced
in all editions of Dehio's Geschichte der Deutschen Kunst; see 1st ed., I,
1919, 25, fig. 37.
Hecht, I, 1928, 27ff and pl. 8 fig. a. Hecht questioned the trustworthiness
of the drawing, because no other monastery churches of
comparable length were attested for the Carolingian period (ibid., 28).
This view is incompatible with the measurements of the abbey church
of Fulda, with a length of 321 feet (see below, pp. 187-89), and was
further weakened by Doppelfeld's discovery under the pavement of
Cologne Cathedral of the foundations of a Carolingian church that was
300 feet long; see above, p. 26, fig. 14, and p. 27.
THE DRAWING NOT THE TITLES
SHOULD BE TRUSTED
A second group of scholars, comprised of Wilhelm 57. Diagram illustrating duodecimal division of Roman and medieval foot, and its 58. Diagram illustrating sedecimal division of Roman and medieval inch, obtained
Effman,[326]
Friedrich Ostendorf,[327]
Ernst Gall,[328]
Edgar
Lehman,[329]
Otto Doppelfeld,[330]
and Wilhelm Rave[331]
chose
to give credence to the drawing rather than to the explanatory
relation to the thumb-breadth of a grown man.
by binary section of each preceding value.

PLAN OF ST. GALL. MONKS' DORMITORY
A. Facsimile reproduction of the red drawing of the Plan (see caption, page 13, vol. III)
B. Same, with 2½-foot module superimposed
C. Probable scheme by which the layout shown in A was constructed
After the area analyzed in Fig. 59, the
Monks' Dormitory embodies the next most
obvious proof that in designing the Plan, the
maker used an accurately graduated scale.
The basic unit of this scale, the 2½-foot
measure, the designer obtained by halving four
times in succession the width he assigned to
the nave of the Church, its transept, and all
the basic claustral structures (see pp. 89-90
and Ernest Born's diagrams and captions,
pp. 92-93).
A 2½-foot module was a felicitous
size for the basic unit of measurement
applying to a settlement the size of the
monastery of the Plan. It was large enough
to account for critical space (seating,
sleeping) and small enough to obviate the
need to draw in excessive detail, and thus to
cloud the view of the community's buildings.
With a practical understanding, the maker
of the Plan rounded up his dimensions to the
next higher—never the lower—module:
furnishings or features that might, when
installed, lay in size between one and another
module, were drawn to the larger size.
This choice was deliberate. The beds of the
Monks' Dormitory, and all other places
where beds are depicted on the Plan (Abbot's
House, House for Distinguished Guests,
Dormitory for Visiting Monks), are examples
of it. All these beds are assigned a width of
one module and a length of three. One module
2½ feet (30 inches) might be considered
adequate for the width of a monk's cot,
but three modules totalling 7½ feet seems
overly long. However, the space of two
modules, 5 feet, would surely have been too
short for a grown man. The longer increment
allowed the designer to indicate just how
many were expected to sleep in a space the
size of the Dormitory; to suggest a possible
bed arrangement while permitting enough
more space to accommodate furnishings; and,
by accumulation of "extra" measure,
ultimately to account for space required by
such constructional features as wall thick-
nesses and staircases, nowhere specifically
indicated on the Plan. Such issues would have
been resolved as a function of supervision
in actual construction, decisions delegated
to an experienced artisan who not only could
understand and interpret the Plan and its
maker's intentions, but who also knew how
to deal with practicalities of building a
wing to house 76 men. More discussion of
these issues is offered, pp. 112-13, and II,
225ff.
60.

walls reconstructed, would have looked as it is shown in
figure 56 (a proposal made by Ostendorf).[332]
Doppelfeld, the most articulate exponent of this group,
has proposed that the inconsistencies between the drawing
and the measurements given in the explanatory titles can
be easily resolved if one were to assume that the scribe who
wrote these legends converted the figure 300 (in Latin,
CCC) into 200 (in Latin, CC) by inadvertently dropping
one of the C's; and that he committed a second error by
confusing a d with an s and thus inadvertently converting
the crucial word bis denos ("twice ten," equaling twenty) of
the intercolumniary legend of the arcades of the nave of
the church into bis senos ("twice six," equaling twelve). If
these errors of the copyist are corrected, Doppelfeld concluded,
all the discrepancies between the drawing and its
explanatory titles would disappear, and the text and drawing
would endorse one another.[333]
Doppelfeld had another reason for believing in the trustworthiness
of the drawing: his own excavations beneath the
pavement of Cologne Cathedral which had brought to light
the foundations of a Carolingian monastery church whose
dimensions were virtually identical to those of the Church
of St. Gall.[334]
THE INCONSISTENCIES NOT PART OF THE
ORIGINAL CONCEPT BUT A CORRECTIVE MEASURE
Doppelfeld's argument was persuasive, and it was based
on a hypothesis subsequently proven to be correct, namely,
that the Plan of St. Gall is not an original but a copy.[335]
Yet
even before this fact was established, Doppelfeld's view
was challenged by Walter Boeckelmann.[336]
The incompatibility
between the drawing and the explanatory titles,
Boeckelmann contended, was not the product of an erring
scribe, but the reflection of a conflict that had arisen at the
council of Aachen, held in 816,[337]
between the bold dimensional
thinking of the old ecclesiastical leaders who had
shaped the policy of the church under Charlemagne and
the constrictive views of the leaders of the reform party
who controlled the church under Louis the Pious. A plan
worked out by the "old guard" had come under the
criticism of the reform party. The dimensions listed in the
explanatory titles were not meant to explain the drawing,
but to correct it. And since the proponents of these corrective
measures did not take it upon themselves to revise the
drawing in the suggested sense, "the disagreement was not
solved in the Plan, the conflict remaining preserved."
Boeckelmann's view, in my opinion, is correct. It reconciles
more of the conflicting traits of the Plan than any of
the previous hypotheses. More recent investigations have
shown that there indeed existed a serious ideological split
at the synods of Aachen between an old conservative group
of churchmen and the leaders of the reform party, which
affected other aspects of the Plan.[338]
CONFLICTING VIEWS ON SCALE OF THE PLAN
But Boeckelmann's theory was challenged, in turn, in
1965 by Adolf Reinle,[339]
who came forth with a new interpretation
of the textual incongruities of the Plan that
departed radically from all views previously expressed on
this subject. The meaning of the axial title of the Church, so
Reinle contended, is not as is generally assumed,
FROM EAST TO WEST
THE LENGTH IS 200 FEET
but rather,
THIS PLAN IS DRAWN AT THE
SCALE OF 1:200
Reinle arrived at this interpretation in the following
manner:
1. PED̄, he maintained, must not be transcribed as
PEDUM (genitive plural of pes = "foot"), but as PEDA or
PEDIA (imperative form of the verb pedare or pediare = "to
measure in feet").[340]
2. LONGĪT̄. must not be read as LONGITUDO (nominative
of the noun longitudo = "length"), but as LONGITUDINE
(ablative form of the noun longitudo = "in length").[341]
3. .CC. is not the simple cardinal figure ducentum =
"two hundred," but must be interpreted as a multiplicative
term, in the sense of ducenties = "two hundred times."
Reinle, accordingly, transcribes the title:
AB ORIENTE IN OCCIDENTEM
LONGITUDINE PEDA DUCENTIES
and purports this to mean
FROM EAST TO WEST, IN LENGTH,
MEASURE TWO HUNDRED TIMES,
or
THIS PLAN IS
DRAWN AT THE SCALE OF 1:200.[342]
This interpretation is untenable on two counts: first, it is
based on an improper textual exegesis; and second, it
ascribes to the ninth century a method of defining architectural
scale relationships that does not antedate the French
Revolution.[343]

61. PLAN OF ST. GALL
CHURCH AND CLAUSTRUM
The 40-foot module is superimposed upon the facsimile
red drawing (shown ½ original size; 1:384)
I have discussed the shortcomings of Reinle's interpretation at
length in a separate study (Horn, 1966, 285-308) and am confining myself
here to a review of my principal objections to his argument.

IMPROPER TEXTUAL EXEGESIS
It is apparent that Reinle's interpretation of the axial title
of the Church has been undertaken without reference to the
Latinity of the other titles of the Plan and their system of
graphical abbreviations. The Plan, as we have seen,[344]
is
furnished with some 340 separate entries of varying length,
the majority in prose, the remainder in verse. The prose is
lucid and not susceptible to misinterpretation at any point.
The verses are often flowery in style, but their syntax and
sense are always clear. There is nothing equivocal about the
distich that defines the interstices between the columns of
the nave arcades (No. 4) or the hexameter that defines the
interstices between the piers of the western Paradise (No.
5). And there is nothing equivocal about the style or syntax
of any of the other titles of the Plan. It is inconceivable
within the total context of these legends that the drafter of
these texts would have framed one of the most crucial lines
of his commentary in so sloppy a manner as to mislead
some seven generations of Latinists into interpreting as a
simple designation of length what he meant to be a ratio of
scale.
If PED̄ had been meant to stand for PEDA, the scribe would
have found himself compelled to make this clear by spelling
the word out—as he had done in title 4 (metire) and title 5
(moderare) where this form is used—in view of the fact that
PED̄ is the traditional abbreviation for PEDUM. By the same
token, he would have had to make it clear that LONGĪT̄
stood for LONGITUDINE, rather than allowing it to be read as
LONGITUDO. And if the capital letters CC were meant to
convey the meaning "two hundred times," rather than the
figure 200, the scribe would have had to make this clear,
since such a use of the letters would have differed distinctly
from their traditional usage. The need for this clarification
would have been the more pressing because clearly all of
the other dimensional titles on the Plan are designations of
simple linear length. No reader of the Plan can fail to notice
that the syntax of the longitudinal title of the Church (No.
1) and the two titles that describe the width of the nave and
the aisles (No. 2 and 3) is identical. Each consists of a
subject (LONGIT[UDO], Latitudo, Latitudo), a prepositional
phrase (AB ORIENTE IN OCCIDENTE[M], interioris templi,
utriusque porticus), and a predicate phrase (PED[UM] .CC.,
pedu[m] xl, pedum xx). The verb est is missing, but is
implicit in the text, and it is, therefore, entirely proper to
translate these respective passages (1, 2, 3, above) as:
FROM EAST TO WEST
THE LENGTH IS 200 FEET
THE WIDTH OF THE NAVE IS 40 FEET
THE WIDTH OF EACH AISLE IS 20 FEET
What was it that induced Reinle to engage in such arbitrary
textual exegesis? This question takes us to our second
main objection:
ANACHRONISM IN MENSURATION
Reinle believes he has discovered that the Plan of St. Gall
was drawn at a scale of 1:200.[345]
He is not the first to
advance this view. Wilhelm Rave had expressed himself
along similar lines in 1956,[346]
and Emil Reisser likewise, in a
study published posthumously in 1960.[347]
The Plan is, indeed, drawn to a scale that comes close to
what we would define today as a ratio of 1:200. But it is one
thing to observe that the Plan was drawn at a scale that
corresponds or comes close to the ratio of 1:200; it is quite
another to claim that it was actually drawn at that scale. In
proposing this view, Reinle is caught in an anachronism.
The concept 1:200 is not a medieval concept and does not
make sense within the medieval system of mensuration. If a
modern architectural drawing is said to be laid out at a
scale of 1:200, this means that one unit on the drawing
corresponds to 200 identical units on the ground. The base
of this ratio is decimal. A medieval architect could not have
expressed himself in these terms, since the two basic units
of measurement with which he worked, the foot and the
inch, were internally divided not into tenths, but into
twelfths and sixteenths (a system that still persists in
England and the larger Anglo-Saxon world) or into
twelfths and twelfths (the pied royal de France, which was
used in France until the introduction of the metric system).[348]
The foot and its primary subdivision, the inch, were
derived from the human body.[349]
Twelve thumb-breadths
of a fully grown man equal the length of his foot (fig. 57).
This is the raison d'être for the twelve units of the English
foot. The French word pouce, the Old French poulcée, the
Latin pollex—all meaning "thumb"—reflect the history of
the genesis of this measure. Like the English foot, the
Latin foot consisted of twelve units[350]
"Inch," Anglo-Saxon
ynce, comes from Latin uncia = "a twelfth"; and
the duodecimal graduation of the Roman foot is reflected
in the series: uncia = 1/12;
| sextans | = 2/12 or ⅙ |
| quadrans | = 3/12 or ¼ |
| triens | = 4/12 or ⅓ |
| quincunx | = 5/12 |
| semipes | = 6/12 or ½ |
| septunx | = 7/12 |
| bes | = 8/12 or ⅔ |
| dodrans | = 9/12 or ¾ |
| dextans | = 10/12 or ⅙ |
| deunx | = 11/12 |

62. PLAN OF ST GALL: SHOWING 40 FOOT MODULE SUPERIMPOSED UPON
THE ENTIRE SITE OF THE MONASTERY

The human body does not offer reliable guidance for
divisions smaller than the breadth of a thumb. These
smaller units could only be obtained by instrumental
operations, and the simplest, easiest, and for that reason,
probably the oldest, way of graduating a distance into a
sequence of consistently decreasing smaller units is the
method of continuous halving—a procedure by means of
which a whole is reduced to a half, a half to a quarter, a
quarter to an eighth, and eighth to a sixteenth (fig. 58).[351]
This is the procedure that created the sixteen graduations
of the English inch.[352]
We know nothing about the internal divisions of the
Carolingian inch, but whether it was graduated into twelfths
or into sixteenths, this much is certain: there was no
common decimal denominator between a Carolingian inch
and a Carolingian foot that could be expressed in the ratio
1:200.
The modern metric scale is based on a comparison of
parts of like nature, all of which can be understood either
as fractions or as multiples of ten. The medieval scale has
no such common unit of reference. It is a combination of a
variety of different forms of graduation (sedecimal, duo-
1. Corporibus. Scilicet non solum de temporibus.
2. Miliarium. Id sunt mille passus. Legua enim ·I· D· passus.
3. Stadium. Id est ·CXXV· passus. Stadium octava pars miliarii est.
4. Iugerum. ·XLVIII· passus. Iugerum est quod possunt duo boves in una
die arare, id est iornalis.5. Perticam. Decem pedes . . .
6. Dimidium. Id est medietas.
7. Semis. Scilicet non solum appellatur medietas librae semis, sed etiam
medietas cubiti et ideo dixit in corporibus.8. Semis. Scilicet ubi semis ponitur, non ponitur et coniunctio.
9. Semissem. Id est dimidium. Accusativus a semis.
"Bede had asserted that the traditional measures had to be adapted to
duodecimals. But the Metz glossator, in introducing these definitions,
gratuitously introduced other schemes of fractions. Granted (2) that a
mile is a thousand paces, a league is 3/2 thousand. A stade (3) is 125
paces, an eighth of a mile. An acre (4) is 48 paces, a rod (5) ten paces. At
this stage of the pattern, medietas (6), the mid-point, becomes a congenial
concept for one half, not only for the semi-pound (7) but for the semicubit,
`and therefore it is used in measuring bodies,' a usage justified
for Bede by no lesser an authority than Moses (Exodus xxv.10) who used
dimidium and semissem in the same sentence interchangably. Hence it
seems that the Metz glossator found it easy, with his mind centered on
the building measurements of Noah's and Moses' arks, to introduce a
scheme of fractions quite at odds with the duodecimalism he was teaching
as the determining ratio of weights and measures."
63. PLAN OF ST. GALL: ONE LINE OF A GRID, 160 FOOT MODULE, FIXED THE CHURCH AXIS

be expressed in the terms of a decimal sequence.
It would be correct to say that the Plan of St. Gall is
drawn to a scale in which one sixteenth of a Carolingian
inch on the drawing corresponds to one Carolingian foot
on the ground. To convert this scale into a relationship in
which the ratio is expressed in the form of like units
requires that the base value of one sixteenth of an inch be
multiplied first by 16 (the sixteen parts of the inch) and then
by 12 (the twelve parts of the foot): 16 × 12 = 192,[353]
the
number of sixteenths of an inch in a foot. The ratio 1:192
is not far from the ratio 1:200, but it is not identical with it
and should, under no circumstances, be confused with it.[354]
In medieval mensuration the scale relationship 1:200 not
only did not exist, it would have been meaningless.[355]
This
fact by itself precludes that the axial title of the Church
could have meant what Reinle purports it to mean, and
thus we are taken back to Boeckelmann's interpretation as
the most reasonable explanation of the dimensional incongruities
of the Plan.
Rave, 1956, 47: "Die Planung des Baumeisters ist geradeso wie
noch meistens unsere heutigen Vorentwürfe im Masstab 1:200 aufgetragen."
For general information see the articles "Weights and Measures"
in Encyclopedia Britannica, and "Poids et Mesures" in Grande Encyclopédie,
XXVI, Paris, n.d., 1184-96, as well as the literature there cited.
Vitruvius, De Architectura, Book 3, chap. 1.5 expresses himself on
this issue as follows: "Mensurarum rationes . . . ex corporis membris
collegerunt, uti digitum, palmum, pedem, cubitum" (see Vitruvius, On
Architecture, ed. Granger, I, 1931, 160ff).
With regard to the Roman foot, see Jacono, 1935, 167-68; for a
fuller account see Hultsch, 1862, 59ff; 1882, 74ff. Of great importance
for the medieval history of the inch is Bede's chapter "De ratione
unciarum" in his De temporum ratione, chap. 4, which Charles W.
Jones brought to my attention. See Bedae opera de temporibus, ed. Jones,
1943, 184-85.
The smallest unit of measure derived from the human body is not the
inch (uncia) but the digit (digitus), the breadth of a finger. It formed the
base of the Italic foot (equivalent to 11.66 modern English inches) which
had sixteen digits. Four digits formed a hand (palmus) and four hands
formed a foot (pes). See Hultsch, loc. cit.
The tenacious survival in the modern Anglo-Saxon world of the
sedecimal graduation of the inch appears to suggest that this was also the
traditional way of subdividing the inches in medieval England. Yet this
is not born out by a reading of chapter 4 of Bede's De temporum ratione
(used as a standard text without rival in Carolingian times), as Charles W.
Jones brings to my attention. Here the inch is defined as being divided
into twelve and even twenty-four parts, a division retained in all of the
Carolingian glosses to this treatise, of which more than forty sets have
been examined by Jones (see Bedae opera de temporibus, ed. Jones, 1943,
loc. cit.). An analysis of Bede and other related texts may in fact suggest
a dichotomy in the approach to duodecimal and sedecimal systems,
between the theoreticians and the practitioners of measures and weights.
Charles W. Jones, in a personal letter, addresses himself to this subject
as follows:
"Bede (A.D. 725) treated weights and measures, primarily the divisions
of pound (libra) and ounce (uncia), in his classroom textbook, De temporum
ratione, chap. iv (Clavis patrum latinorum, n. 2320; see also Pat. Lat. XC,
cols. 699-702). Therein he recognized no other fractional principle than
duodecimalism, despite his addiction as an exegete to the concept of ten,
its square, and cube. He positively states that duodecimals are used not
only for weights (including numismetrics) but also for times (months,
hours, points, moments) and for lines, planes, and volumes of bodies
(Jones, 1943, 184.2-3; 185.26-28, 44-49).
"I have examined about twenty different sets of glosses for that
chapter, but only the following sets contain remarks pertinent to this
topic: Berlin MS 130, written A.D. 873 at Metz; Munich MS 18158, an
eleventh-century copy from Tegernsee of a ninth-century text; 21557, an
adaptation of 18158; Valenciennes MS 174, written about A.D. 840 at
Saint-Amand (duplicated in Brussels MS 9837-9840, saec. xii/xiii);
Vatican MS Rossi lat. 247, copied in the Loire region [Fleury?] about
A.D. 1018 from an exemplar of ca. 820. (The complete set of glosses from
the Berlin MS will be published in the forthcoming Corpus Christianorum
edition of Bede's Opera didascalica.) Bede's was the basic text on
the subject in Carolingian schools: about 150 codexes containing that
chapter are extant today. The masters seem to have disregarded Isidore's
treatment, Etymologiarum liber XVI, xxv-xvii, although it was in common
circulation. But they do quote Priscian's De figuris numerorum liber ii,
9-iii, 16 (ed. H. Keil, Grammatici Latini III, Leipzig, 1859, pp. 407-11),
sometimes verbatim and several times by name. Priscian dealt with
both decimals and duodecimals, but the glossators quite obviously tried
to eliminate decimalism by recasting his statements. Nor, with one
exception which I will mention, did these glossators introduce any
suggestion of sedecimalism.
"In short, the scholastic evidence points exclusively to duodecimal
measures in Carolingian as in early-English times.
"Such proof by silence might seem to refute use of sedecimals, but we
know that medieval scholasticism often was remote from practice. An
analogue is the void between Boethian and Gregorian music. I agree with
you that a master builder, with rod and plumbline, would be apt to
think in multiples of halves. The Metz glossator (Berlin MS) seems to
lend some support to this surmise. Bede had stated; Item decorporibus,
sive miliarium, sive, stadium, sive iugerum, sive perticam, sive etiam cubitum,
pedemve aut palmun partiri opus habes, praefata ratione facies. Denique et
in Exodo dimidium cubiti semis appellatur, narrante Moyse, quod habuerit
arca testamenti duos semis cubitos longitudinis, et cubitum ac semissem
altitudinis. ("Also you hold to the same fractions in measuring bodies,
whether miles, or stades, or acres, or rods, or even cubits, feet, or hands,
whenever you need to divide. In fact, in Exodus a half cubit is called a
`semis,' because, according to the statement of Moses, the Ark of the
Testament was two and a half cubits in length and a cubit and a half in
height.") The Metz glossator writes:
That the Plan of St. Gall was drawn to a scale of 1/16″:1′ was first
expressed by me in the French edition of the catalogue to the Council of
Europe exhibition dedicated to Charlemagne: "Le plan est entièrement
dessiné d'après une échelle, ou le 1/16e d'un pouce sur le parchemin
représente un pied sur le terrain. Converti en une relation d'unités
egales, cela signifie 1:192 (1/16 × 16 × 12 = 192/16), rapport de grandeur
qui approche l'échelle métrique du 1:200, mais qu'il ne faut aucunement
confondre avec celle-ci; puisque la relation 1:200 n'existait pas dans le
système métrologique médieval, où le pied est divisé en 12 pouces, et le
pouce en seize seizièmes" (see Charlemagne, oeuvre, rayonnement et
survivances [Dixième Exposition sous les Auspices du Conseil de
l'Europe], ed. Wolfgang Braunfels, Aix-la-Chapelle, 1965, 399).
I am delighted to find that in an article that became available to me
only after the present study was completed, Konrad Hecht had independently
come to the same conclusion: "Der Masstab 1:200 ist für einen
mittelalterlichen Plan zwar plausibel, aber doch irrig, denn dieser Masstab
setzt die dezimale Teilung des Fussmasses voraus. . . . Der St. Galler
Plan wurde nicht im Masstab 1:200, sondern im Masstab 1/16″:1′ entsprechend
1:192 gezeichnet" (Hecht, 1965, 187-88).
The figure 200 is not a natural break in a system that is based on
fractions of 12 and 16. It acquired meaning only after the adoption of the
metric system—a system of consistently graduated units of like dimension
which departed so radically from the chaotic, but deeply ingrained,
forms of mensuration which it supplanted that it could have been
inaugurated only under the auspices of a political revolution and enforced
by the mandate of an ensuing dictatorship. For a brief résumé of the
adoption of the metric system, see Arthur E. Kennelly, 1928, 12-27; for
a comprehensive, detailed account of the establishment and propagation
of the metric system and the operations that determined the meter and
the kilogram, see Favre, 1931 and Bigourdan, 1901.
EARLY EXPRESSION OF THE VIEW THAT
THE PLAN WAS DRAWN TO A CONSISTENT SCALE
In contrast to those who held that the Plan of St. Gall
was purely a schematic rendering, Boeckelmann believed
that the Plan was drawn to a definite scale and that the key
to this scale was to be found in the 40 feet that the draftsman
ascribed to the width of the nave of the Church. He
observed that values consistent with this scale can be recognized
in the dimensions of many other areas of the Plan.
The Cloister Yard, for example, if measured in the light of
the 40-foot width of the nave, forms a square of 100 feet;
the rectangular area in its center, a square of 20 feet.[356]
Boeckelmann was not the first to make this observation.
As early as 1938, Fritz Viktor Arens had drawn attention
to the fact that many of the dimensions of the Plan of St.
Gall were based upon a decimal system consistent with the
40-foot width of the nave of the Church.[357]
He also observed
another important fact, that if one attempted to
redraw the Plan of St. Gall in the light of the measurements
given for the length of the Church (200 feet), the Cloister
and all service structures of the Plan would be reduced to a
size in which they could no longer perform their designated
functions.[358]
It was the most stringent argument in favor of
the assumption that if any of the measurements given in
the explanatory titles of the Plan reflect the original scale,
it is the 40-foot figure listed for the width of the nave, and
not the 200-foot figure listed for the length of the Church.
Arens' and Boeckelmann's observations were fundamental.
Yet neither Arens nor Boeckelmann realized their
full significance. Their failure to do so was probably caused
by their awareness that, whereas the dimensions of many of
the larger installations of the Plan can clearly be interpreted
as multiples of ten, many others—and in particular the
majority of all the smaller dimensional values of the Plan—
are inexplicable in the context of a decimal scale.
Ibid., 66-67. Arens drew attention to the fact that the dimensions of
the beds in the Monks' Dormitory make perfect sense if interpreted in
the light of the 40-foot width of the nave of the Church, but become
unrealistic if related to the 200 feet stipulated for the length of the
Church. Emil Reisser (1960, 53) came independently to the same conclusions:
"Eine von mir vorgenommene Nachprüfung hat ergeben, dass
man mindestens das im St. Galler Plan eingeschriebene Mass von 40
Fuss (zu 0.33) = 13.20 Meter für die Mittelschiffsbreite der Kirche . . .
annehmen muss, wenn die Räume der übrigen Bauten eine brauchbare
Grösse erhalten sollen." My own analysis of the Plan confirms this
observation. Not only would the monks, including the Abbot and the
visiting noblemen, no longer fit into their beds, but the Refectory would
be too small to seat the monastery's contingent of monks, the horses
would lack the required floor space to stand in their stables, the workmen
could not carry out their crafts and labors. The Cloister Yard would be
by one third below what Hildemar, a ninth-century monk, defined as the
desirable minimum (cf. below, p. 246).
I.14.3
SCALE USED IN DESIGNING THE
PLAN
A WORD OF CAUTION
In turning, at this juncture, to an account of my own conclusions
on the scale that was used in designing the Plan, I
should like to start with a word of caution. While I hold the
view that the Plan was drawn to a definite scale, and that
this scale was applied consistently throughout the entire

64. PLAN OF ST. GALL. MONKS' VEGETABLE GARDEN
The vegetable growing plots measure two
modules wide, 5 feet (60 inches) and would
require a reach of no greater than 30 inches
from the work space between plots, an
efficient size for hand cultivation. The clear
work space between the cultivated strips, 1-1½
modules wide (45 inches) was adequate for
a gardener with barrow or basket.
The center aisle, 2 modules wide, permitted
two men with their barrows or vegetable
baskets to easily pass each other.
The planning stresses no waste motion, no
scattered lost effort. This was not a garden
in which to play at gardening. It was close
to life, the need to live and the desire to
live. Nowhere in the Plan is the sense of
urgency, the necessity of collaboration and
conservation of resources more dramatically
and concisely expressed than in this simple
composition of eighteen rectangular garden
plots. Adjacent, on the north, where fruit
ripened for the monks' table, was the Monastery
Orchard which served a second purpose
as the Monks' Cemetery (always efficient
even in death) where the monks took their
long final rest.
Modularity was born of sacred numbers.
Each was but a finite and measureable
feature of divine and infinite order communicated
to men from heaven by a vast
scheme of symbolism. The passion for order
still persists, but the explanations are not the
same.
For extended treatment of the Monks'
Vegetable Garden see II, 204, 205.
Cemetery and Orchard are treated on page
211, vol. II.
Characters in black squares identify buildings
of the Plan, page xxiv, and III, 14
(Catalogue of Inscriptions).
E.B.
A submodule grid of 1¼ feet is superimposed on the plots of the vegetable garden (red drawing, same size as original; scale 1:192)

could expect to be able to determine without any shadow of
doubt the precise dimensions of every building, or any piece
of furniture, shown on this scheme. This is impossible for a
number of reasons. Most important among these are that
the Plan is not an original but a copy, and that this copy was
traced, without the aid of any supporting instruments,
through the opaque body of large and rather unmanageable
pieces of parchment that had to be held against a light
surface in order to acquire the requisite transparency.[360]
This was bound to introduce a multitude of minor inaccuracies
and inconsistencies that are incompatible with the
precision of draftsmanship required in the development of
the original scheme.
Moreover, there is clear evidence, as I have demonstrated
elsewhere, that in the process of tracing, original and overlay
changed their respective positions, in several instances
causing a substantial measure of distortion. This is noticeable
especially in the alignment of the claustral structures
with the Church and in the distorted layout of the stables in
the southwestern corner of the settlement.[361]
Despite these malformations, minor or major as they
may be, the Plan of St. Gall retains enough of the precision
of the prototype to permit the conclusion that the original
was based on a consistent and carefully calculated scale, and
to allow us to reconstruct the basic graduations of this
scale.
The primary reason why this problem was not solved in
the past is, I think, that most of the students who took an
interest in this matter were Continental Europeans reared
on the metric system. Being raised in this system, I, too,
could not avoid interpreting the scale of the Plan—as I
presume many others tried before me—by constructing a
straightedge on which the value forty (width of the nave)
was graduated into forty equal units. Applying this scale to
the various buildings of the Plan as well as to the open
spaces between them, I recognized quickly, yet not without
consternation, that a staggering majority of the dimensions
appeared to coincide with intermediate values that did not
make sense in terms of an even numerical progression. I
was puzzled by the frequent occurrence of such values as
2½, 7½, 12½, 17½, 22½, 27½, and so on, and in a special sense
by the heavy recurrent rate of what appeared to be a
standard value, namely, the width assigned to the steps,
benches, and beds. It was larger than 2, yet smaller than 3,
and appeared to make sense only if interpreted as 2½.
I was puzzled by these observations until it occurred to
me that the conditions that they reflected might be related
to the possibility that the inventor of the scheme availed
himself of a scale that was not based on the continuous
sequence of equal numerical values used in the decimal
system, but emerged from the geometrical thinking of the
developmentally older sedecimal system that survives in the
subdivisions of the English inch. I consequently designed a
scale in which the value 40 was internally graduated into
sixteen units, each of a length of 2½ feet, and the entire
riddle of the Plan unfolded itself.
I shall demonstrate the validity of this assertion with a
scale analysis of two areas of the Plan which lend themselves
with particular ease to this type of investigation.
The core of the views advanced on the following pages were first
presented by me in a paper read at the International Symposium held at
St. Gall in the summer of 1957 (reviewed by Poeschel, 1957, 9-29; Idem.
in Studien, 1962, 27-28; by Bessler, 1958; by Doppelfeld, 1957; by
Gruber, 1960; and by Knoepfli, 1961, 312-14.
I have touched in print upon these problems briefly in Studien, 1962,
94-95 as well as in the catalogues of the Council of Europe Exhibition
Karl der Grosse, ed. Wolfgang Braunfels, Aachen, 1965, 409-10 (French
edition, p. 399); and in more detail in an article entitled "The `Dimensional
Inconsistencies' of the Plan of St. Gall and the Problem of the
Scale of the Plan," published in The Art Bulletin, XLVIII, 1966, 285308.
An abridged version of this article was read at a meeting of the
Herbert M. Evans History of Science Dinner Club, on 2 January 1968.
It was in the ensuing discussion that Professor Charles L. Camp remarked
on the similarity of the series 640, 160, 40, 10, 2 1/2 of the Plan of St.
Gall with the American land measuring system of 1785, an observation
in the pursuit of which Hunter Dupree made the fascinating historical
discoveries reviewed in III, Appendix III.
THE 2½-FOOT MODULE (STANDARD MODULE)
Figure 59 shows a scale analysis of the southern transept
covered by this part of the Church forms a square, each
side of which is equal to the width of the nave, i.e., 40 feet.
In the second and third drawing shown on this page, this
square is subdivided into sixteen strips, first from north to
south, then from east to west; in the last drawing the two
systems are combined.
The experiment proves that all the internal area divisions
of the southern transept arm are conceived as
multiples of a 2½-foot square. The passageway that gives
access to the crypt is three units wide and sixteen units long
(7½ × 40 feet), the platform on which the altar of St.
Andrew stands is three units wide and ten units long
(7½ × 25 feet). The steps and benches have a standard
width of one unit (2½ feet) and vary in length between five,
six, and ten units (12½ feet, 15 feet, and 25 feet). The
intervals between the steps and benches likewise can be
brought into a system of logical relationships, if interpreted
as multiples of a 2½-foot square.
An analysis of the adjacent area of the Dormitory of the
Monks (fig. 60.A) enables us to establish this point with
beds in this building is inconceivable without the use of a
carefully constructed system of auxiliary construction lines.
It is easily understandable if it is conceived as being developed
within a grid of 2½-foot squares (demonstrated in fig.
60.C). The overall analysis of Cloister and Church suggests
that the building was meant to be sixteen 2½-foot units wide
and thirty-four 2½-foot units long (40 × 85 feet). Each bed
is one unit wide and three units long (2½ × 7½ feet), with

65. PLAN OF ST. GALL. KITCHEN AND BATHHOUSE OF THE ILL
A 1¼-foot module grid is superimposed on this detail from the facsimile red print (scale 1:192, original size).
walls which had to be shortened to leave sufficient room for
the entrances and exits located in these walls. A glance at
the drawings shown in figure 60.B discloses that the boundaries
of the beds do not in all cases coincide with the
boundaries of the underlying squares. The beds that lie at
right angles to the long wall straddle the grid lines with
their center axis. This suggests the possibility of the use of
an even smaller module, which we shall discuss later.
The superimposition of the square grid on the original
drawing (fig. 60.B) reveals the means by which the draftsman,
in copying this building, extended its length by one
unit beyond what it was meant to be through an accumulation
of small errors. The center group of beds in the northern
half of the Dormitory has a length of twelve 2½-foot
modules. The corresponding group of beds in the southern
half of the building is thirteen 2½-foot modules long. It is
obvious that they were meant to be of identical size. Figure
60.B shows with great precision those places where the
draftsman took on these additional increments of space
(first and second transverse row in the southern half of the
building). This was probably due to two slight and almost
imperceptible shifts in the relation of the original parchment
to the tracing sheets. By the time the draftsman had
reached the end of the second row of beds, he had inadvertently
picked up an excess of an entire module. This lengthened
the Dormitory from thirty-four to thirty-five standard
modules, or from 85 feet (length of the original) to 87½ feet
(length of the copy).[364]
In analyzing the dimensional layout of this as well as any
other building of the Plan it is important that the overall
dimensions of each respective structure be ascertained by
its relation to neighboring or superordinate units before an
attempt is made to decipher its internal relationships.
Hecht (1965, 175) observed that the square grid of the schematic
drawing of the Dormitory, which I published in Studien, 1962, 91, fig. 7,
is by one standard module shorter than the drawing (16 × 34 units); he
tried to correct my "mistake" by a square grid measuring 16 × 35 units.
The mistake is not mine, but that of the monk who traced the Plan of
St. Gall.
THE 40-FOOT MODULE (LARGE MODULE)
This module controls the proportions of the Church and
the layout of the Claustrum (fig. 61). The transept and
nave of the Church, being of equal width, by necessity form
a square at their area of intersection. As is the case in
certain Romanesque churches of Normandy and the Rhineland
two centuries later, the dimensions of this square
determine the layout of the remaining portions of the
church. Thus on the Plan of St. Gall the transept of the
Church forms an oblong composed of three times the area
of the crossing unit. The nave is a space composed of
four and one-half such units, while three more units of
identical size are added to the east of the transept; the forechoir,
the sacristy, and the library. It should be noted that
in the nave the squares are arranged in such a manner that
the corners coincide with the axis of each column. The 40
feet assigned to the width of the nave must for that reason
be interpreted to relate not to the clear span between the
bases of these columns, but to the distance from axis to axis
of each corresponding pair of columns.
That the Church of the Plan of St. Gall is laid out
according to a system of squares has been observed by

to have been entirely overlooked is that the entire aggregate
of buildings forming the Claustrum is developed in a
similar manner.
A glance at figure 61 shows that the body of the Church
can be inscribed into a grid of 40-foot squares (three units
wide and nine units long), and the claustral structures that
abut the Church to the east can be entered into an adjacent
grid of identical squares (three units wide and five and one-half
units long). I have no doubt that this is the manner in
which the drawing was started. But attention must be
drawn to the fact that the alignment of the drawing with the
grid is not perfect. There are two discrepancies—not large,
yet conspicuous enough to cause some concern.
One of these is that the aisles of the Church are not 20
feet wide, as one should expect them to be in the light of
their explanatory titles (latitudo utriusque porticus pedum xx);
instead they measure 22½ feet. The other is that in certain
places the Dormitory and the Refectory extend over the
southern boundaries of the 40-foot grid of the Claustrum
by as much as 5 feet. I believe that these deviations are the
result of purposeful modifications undertaken as the drawing
progressed from its initial conception into its final
stages; and I shall discuss this point in detail later.
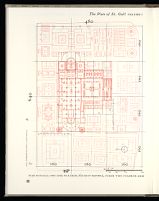
THE 160-FOOT MODULE (SUPER MODULE)
The discovery that the Church and the Claustrum were
designed ad quadratum raises the question of whether the
site plan for the entire monastery may not have been
developed from the dimensions of the crossing square. To
answer this question is not easy, because the Plan of St.
Gall fails to inform us about the location of the walls that
separate the monastery from the secular world. We do not
know where the grounds of the monastery begin and where
they end. It is probable, however, that this problem may be
solved by a simple proportional speculation.
Measured from west to east—or more precisely, from the
westernmost fences of the agricultural service structures
west of the Church to the easternmost lines of the building
masses east of the Church—the monastery grounds are
sixteen times the width of the nave of the Church (640
feet), a round and very convincing number, in which the
figure four plays a determinant role (fig. 62). By contrast,
the distance between the outermost lines of the building
masses sited along the southern edge of the monastery and
the outermost lines of the building masses on the northern
side amounts to 11½ times the 40-foot width of the nave of
the Church (fig. 62). The proportion 11½:16 is not a likely
medieval relationship. A more convincing proportion would
be 12:16 (or 3:4). There is some evidence, not easily discarded,
which suggests that in the south and north the
monastery grounds were meant to extend beyond the outer
building masses, since the fences of some of the buildings
located along the southern and northern border of the
monastery site run out into the space which lies beyond
these structures, and end only at the end of the parchment.
Two such fences, running north, may be seen on either side
of the Outer School; another runs south in extension of the
west wall of the House for the Workmen (fig. 62). There
are other considerations of a practical nature which would
require a buffer zone between the outer building lines and
the monastery wall. The water-driven machinery of the
Mill and Mortar houses are dependent on flues and sluices
that can only have run to the south of these buildings, and
a similar safety margin of space would have been desirable
in the north for servicing the privies.
A buffer zone of 10 feet added to the building masses, on
either of the two long sides of the Plan, would take care of
these necessities and would result in a meaningful overall
proportion (12:16 or 3:4) for the Plan (fig. 62). The
acceptance of such an overall modular scheme would,
moreover, help us to settle two other puzzling aspects of
the Plan.
It would explain the location of the Church. It has never
been clarified why the Church lies where it does on the
Plan. It is obvious that it had to be off-center. Had it been
placed in the center of the Plan, the southernmost buildings
of the Claustrum would have been moved to the southern
edge of the monastery, leaving no room for the subsidiary
claustral structures, such as the Monks' Bake and Brew
House, the Mill, and the Mortar. But what determined the
exact distance by which the axis of the Church was to be
off-center?
If we assume that the monastery site was calculated as an
oblong, sixteen 40-foot modules long and twelve 40-foot
modules wide, the entire monastery site could be conceived
as having been inscribed into a grid of twelve supersquares,
each formed by four 40-foot squares, and therefore measuring
160 × 160 feet (fig. 63). Within the linear frame of
reference established by such a grid the difficult problem
of the axial position of the Church—incomprehensible in
terms of the layout of the Roman castrum, with which it has
frequently been compared—would find a surprisingly
simple explanation. The axis of the Church would coincide
with the first, the axis of the Refectory with the second of
the two longitudinal lines of the grid.
The same grid would also explain the transverse division
of the monastery into its four principal building sites:
A western zone, accommodating the houses for livestock
and their keepers and two houses to take care of the
knights and servants who travel in the emperor's following;
A central zone, of twice the surface area of the western
zone, accommodating the Church, the Claustrum, and
all of the buildings that lie to the north and south of this
complex;
An eastern zone, coequal in surface area with the western
zone, accommodating the Novitiate and the Infirmary,
the Cemetery, and several other installations.
The western and eastern group of buildings are each
inscribed into a surface area formed by three 160-foot
squares; the central block of buildings extends over six.

DIAGRAM I THE SEQUENCE OF PROGRESSIVE DICHOTOMY USED IN THE SCHEME OF MEASUREMENTS
EMPLOYED IN THE DESIGN AND DRAWING OF THE PLAN
The standard module, 2½ feet, is obtained by successively halving the large module (40 feet) four times. The value of the exponent, column B, indicates the number
of times that the number 40 has been halved. The procedure shown here that yields successively smaller units of measurement, decreasing from 40 feet to
2½ feet by successive halving is "reversible," and is reversible by the same pattern of geometric progression shown here, but in the "opposite" direction yielding
progressively larger values.
Thus larger modules, multiples of 40 feet, such as 160 feet and 640 feet, are evolved from the same standard module and using the same pattern of development.
This is illustrated on the opposite page in Diagram II.
In Diagram II one can visualize the grand symmetry of the scheme of measures by which the design of the Plan was ordered and controlled. For example, 640
is symmetrically disposed with respect to 2½ about the sacred number 40 taken as a pivot or point of origin. In the pattern of such a formula, the infinitely great
and the infinitely small participate with equal significance, in a scheme, it seemed, of divine order. The crossing square, four equal sides each of 40 feet, indeed
defined a holy space.
Forty, the number of greatest value in the series of NUMERI SACRI, was chosen by the designer of the Plan of St. Gall as that dimension in feet
for the crossing square of the Church, the holy space unsurpassed in meaning and felicity to all inhabitants of the monastery.
It was clearly discernible from tracing drafts, in our study of the Plan, that 160 feet, four times forty, was the major module of the Plan.
This is the largest measure which is a common multiple of the Plan. Four units of this module, or 640 feet, is the length of the Plan, and three
units of this module, or 480 feet, is the width of the Plan.
The reason that the 160-foot module, four times the 40-foot dimension of the crossing square, was chosen as a module may be understood by
perusing Diagrams I and II, giving attention to the numerical sequences in columns A, B, C, in each figure. Diagram I portrays a
progression of halving starting with the 40-foot module and DESCENDING to 2½ feet. Diagram II starts out with the 40-foot module, extends the
geometric series in the opposite upward direction by doubling.
The values obtained by doubling, from 40 to 160, correspond at each level of ascent, to the smaller values obtained by the descent from 40 to
2½ feet. The bar elements of Diagram II illustrate the progression graphically: however, it is Column B that cogently reveals the homogeneity
of the numerical relationships as a scheme that established the intrinsic pattern of measurements used in the Plan of St. Gall.

DIAGRAM II THE SUPERMODULE, 160 FEET, ITS DERIVATIVES, 640 FEET AND 480 FEET, AND ITS
RELATIONSHIP TO THE LARGE MODULE
† 640 is the "height" or east-west dimension of the Plan
* 480 feet, the "width," or north-south dimension of the Plan, is an element in this geometric progression. It is derived by taking the sum of the two elements
of the progression 320 & 160, or 3 × 160. With sacred numbers 3 and 4 as multipliers and 160 as a multiplicand, 480 and 640 emerge as the dimensions, in feet,
of the Plan. Sacred numbers, NUMERI SACRI, are treated extensively under I.17, page 118; see also remarks, caption, page 109.
We noticed that, out of the scared number 40, the values of 2½, 10, 40, 160, 640 are generated by exponential values of 4, 2, 0, -2, -4.
Although the more sophisticated notation of Column B was probably not common knowledge in the 9th century, the notation of Column C was
understandable. There is no magic in this simple observation. But it is apparent that the multiplier 4, operating on 40 and yielding 160 was not
chosen by caprice. A module less than 40 facilitated the arduous work of design.
The number 480, 3 times 160, is not one of the natural steps of the progression between 2½ and 40, as shown in DIAGRAM II. This strongly
suggests that the CAUSA PRIMA of the dimension system of the Plan was the longitudinal axis of the Plan of the Church, extended to east and
west to satisfy designing a plan of paradigmatic significance and future influence. The axis of the Church was extended one module of 160 feet to
the east (of the front line of the altar of St. Paul) and one module of 160 feet to the west of the entrance to the covered walk of the west paradise.
This established the length of the Plan, four modules of 160 feet or 640 feet. One module of 160 feet north of the axis and two modules of 160 feet
south of the axis gives three modules of 160, or 480 feet, the width of the Plan. That the dimensions of the Plan are in the proportion of 3 to
4 was more than good theology. The numbers 3, 4, and 5 are the key to accurate construction of a rectangle in land surveying and in building
construction.
E. B.

THE CAROLINGIAN MEASURE AND SCALE USED IN DESIGNING THE PLAN
On the basis of the calculations listed below we compute the length of the foot used in designing the Plan to have these equivalents:
In English and U.S. standard measure: 1′ ⅝″.
In metric measure: 32.07cm
This computation can only be understood as an approximation of the real Carolingian foot that the draftsman of the Plan himself used. The computation
must be corrected, first by the diminution in size to which the parchment was subjected through shrinkage throughout the ages of its existence, and second,
minor distortions caused by shrinkage of photographic elements in development, or of the paper on which the facsimile was printed, during drying.
Our computation of the "foot of the Plan" as reflected in the Löpfe-Benz facsimile is based on an analysis of the longest clearly measurable dimension shown
on the drawing, namely the span extending from the center of the arcade columns that stand at the entrance wall of the church to the center of the columns
that form the easternmost boundary of the crossing square. This span encompasses five and one-half 40-foot squares and consequently represents a length of
220 "Plan feet". Owing to uneven shrinkage or irregularities in the drawing this distance varies slightly depending on whether it is measured along the axis
of the northern, or of the southern row of nave arcades. Using an engine-divided scale of good manufacture with 16 divisions to the inch based on the U.S.
standard foot (identical with the British standard foot) we arrive at the following figures:
231 + 232/2 = average value = 231.5 units (measure on south row = 232 units of 1/16 inch, measure on north row = 231 units)
231.5/220 = 1.05227 feet—12⅝ inches—32.067 cm
This is the measure of the foot of the Plan.
[computation: 12 inches = 30.480 cm.
⅝ inch = 1.587 cm/32.067 cm]

THE 1¼-FOOT MODULE (SUBMODULE)
There is good reason to assume that in certain installations
the inventor of the scheme made use of a submodule by
halving his standard module of 2½ feet, thus arriving at the
smallest module of 1¼ feet. I refer to this unit as a "submodule"
because it is used sparingly, in contrast to the
2½-foot unit which is used as a standard module throughout
the length and width of the Plan. I have pointed out that
2½ feet is one sixteenth of 40, the width assigned to the
nave of the Church; 1¼ is one thirty-second of this measure.
The peculiar values 2½ and 1¼—strange to anyone accustomed
to working with a metric scale—will ring a more
familiar tone if it is remembered that these units correspond
to 30 and 15 inches.
The Plan contains a number of installations which cannot
be explained in any other manner than on the assumption
that they have been constructed on a 1¼-foot module. We
have already encountered it in our analysis of the Dormitory
submodule, however, is in the Monks' Vegetable Garden
(fig. 64).
The Garden covers a surface area that is twenty-one
standard 2½-foot units wide and thirty-three standard
2½-foot units long (52½ × 82½ feet). It consists of two rows
of planting beds, nine on either side, made accessible by a
carefully designed system of paths: three running lengthwise,
ten crosswise. The planting beds are 5 feet wide and
20 feet long. The width of the crosspaths by which they are
separated is less than 5 feet but more than 2½ feet. The
only logical way to relate nine planting beds 5 feet in width
to ten paths the width of which is less than 5 and more than
2½ feet within the available surface area, is to assume that
the draftsman conceived this layout within a grid of squares
of one-half the value of his standard square, i.e., a submodule
of 1¼ feet. This module would allow him to
develop the respective width of the planting beds and the
paths with absolute precision, lengthwise in the simple
sequence of
3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3 · 4 · 3,
and crosswise in the sequence of
3 · 16 · 4 · 16 · 3.
The 1¼-foot module is also used in the Kitchen and Bath
houses of the Novitiate and the Infirmary (fig. 65). These
buildings are each nine by eighteen of the 2½-foot modules.
They are internally divided into two coequal squares of
nine by nine 2½-foot modules, one containing the Bath
House, the other the Kitchen. The hearth in each of these
two installations forms a square that is composed of four
2½-foot modules. To place a square of four 2½-foot modules
concentrically into the interior of a square of eighty-one
2½-foot modules is possible only within the framework of a
1¼-foot grid. In such a grid each side of the Kitchen and
Bath House would be graduated into eighteen units of 1¼
feet. The position of the hearth could be struck off with
absolute precision in the sequence 7 · 4 · 7; the position of
the bath tubs, with their diameter of three submodules, in
the sequence 2 · 3 · 2 within the squares of seven submodules
left in the four corners.
There are four or five more buildings on the Plan—not
counting several smaller areas here and there—in which the
submodule appears to have been employed (Abbot's
House, House for Distinguished Guests, cloisters of the
Infirmary and the Novitiate, and possibly the Refectory),
but to interpret how exactly it was used in each case is
difficult because the module is so small. A distance of 1¼
feet on the Plan amounts to not much more than twice the
thickness of the stroke of the quill with which the Plan was
drawn. Since the lines were traced without the aid of a
straightedge, even the slightest irregularity in the movement
of the hand would tend to blur the intent of the
original scheme. Therefore, rather than weakening the
argument by interpreting details which may be susceptible
to different solutions, I should like to confine myself to
establishing that this module was used by focusing on
those areas in which its existence can be clearly demonstrated.
I.14.4
THE SCALE OF THE PLAN
AND ITS RELATION TO THE
CAROLINGIAN FOOT
Having established that the Plan was drawn to a consistent
scale we must then ask whether this scale was invented for
this specific purpose, or whether it was related to any
regular Carolingian system of measurement. I believe that
the original scheme of the Plan of St. Gall was drawn with a
regular Carolingian straightedge, 40 Carolingian inches
long, and that the designer of the scheme established the
overall dimensions of the monastery site by assigning to it
a length of 40 and a width of 30 Carolingian inches.
The modern English foot is the equivalent of 30.48 cm.
The classical Roman foot was 29.60 cm. The Carolingian
foot was larger and, despite Charlemagne's attempt to
standardize weights and measures, appears to have been
afflicted by a good deal of regional variation. Kutsch,
Schmidt, and Behn in measuring Carolingian churches
believed that they were able to establish its length as 34.00
cm.; Hanftmann and Arens as 33.29 cm.; Rave as 33.3033.50
cm.; and Doppelfeld as 30.04 cm.[367]
The studies of
Felix Kreusch[368]
and Leo Hugot[369]
suggest that the Palace
Chapel at Aachen was built on a Carolingian foot whose
length corresponded to 33.30 cm. This is the exact equivalent
of the old Drusian foot, which the agrimensor Hyginus
tells us was in use in the territory of the Tungri[370]
and which
Drusus adopted from the Belgians as a northern standard
for the border settlements of the Agri Decumates. This foot,
two digits longer than the Roman foot, appears to have
been the traditional standard measure of the Franks and
may have formed the base of the commonest building foot
used in medieval France and England.[371]

67. PLAN OF ST. GALL
No other drawing shows the unique conceptual elegance
of modular design to any higher degree of purity and
perfection: the dimensioning of the two intersecting spatial
volumes of nave and transept as multiples of a 40-foot
square, and determination of the width of the aisle in
an ingenious division of the 40-foot measure (16 modules of
2½ feet) as is shown in figure 67.
Possibly, in a preliminary draft of the Plan, the aisle
had been taken by the designer as one half of the nave width.
This could account for the inscription PEDUM XX (see caption
for figure 68). Further consideration, probably of a
pragmatic nature, resulted in the aisle width adopted,
3 + 3 + 3 units—3 modules for the width of the aisle
altars and 3 modules clearance space on each side of each
altar. This method of division gave a splendid trinity of
threes, with 7 modules left over, all in admirable conformity
with St. Augustine's admonition on number (page 118).
This illustrates well how a scheme of modularity can be
selectively manipulated to yield relationships of some
complexity, variety and interest, quite removed from unmitigated
repetition of the same measure, inherent in a grid of
equal divisions. The grid can be banal, but it need not be.
Imaginative manipulation of the sacred number dogma as
seen here, while not exactly typical practice, besides
revealing cognition of alternatives to monometric
schematism, responds to exigencies of a situation. Theology,
liturgy, convenience, amenity, and structure, needed to be
resolved in an effective layout, and were.
Figure 67 notes the concept as it existed in the author's mind
before modifications that would have to be made in places
where a purely intellectual concept—easy to express in a
simple line drawing—came into conflict with progmatic
realities such as allowances for wall thickness. Such conflict
was inevitable where two buildings shared a common wall
in which case the space needed for masonry would have
to be subtracted from the interior of these buildings rather
than from the open areas around them.
STEP 1: CONSTRUCTION OF THE LAYOUT OF THE MONASTERY CHURCH

The foot used in the Plan of St. Gall, if calculated on its
present dimensions, amounted to 32.16 cm. However,
attention must be drawn to the fact that the parchment on
which the Plan is drawn was subject to a considerable
amount of shrinkage. Even today, as Dr. Duft has observed,
when displaying the Plan in its showcase, the surface of the
parchment expands and contracts in response to the
changing humidity content of the air. Konrad Hecht, who
has made some interesting observations on this subject[372]
estimates the mean loss by shrinkage to which the Plan was
exposed through the ages to be 5 to 6 percent. If we modify
the figure obtained from the present shrunken surface of
the Plan by this quotient, the metric equivalent of the
Carolingian foot which was used in the Plan is more likely
to have been around 34.00 cm., which would conform to
the findings of Kutsch, Schmidt, and Behn. It could
equally well have been the exact equivalent of the old
Drusian foot of 33.30 cm., which appears to have been the
historical prototype of the Carolingian foot.
Tabulated in their respective order of magnitude, the
relation of the graduations shown on the straightedge used
in designing the Plan to the actual dimensions for which
they stood are as follows:
1. Dimensions of the entire monastery site:
30 × 40 Carolingian inches = 480 × 640 feet.
2. Super module:
10 × 10 Carolingian inches = 160 × 160 feet.
3. Large module:
2½ × 2½ Carolingian inches = 40 × 40 feet.
4. Standard module:
one sixteenth of 2½ Carolingian inches (i.e., one
sixteenth of 40 feet) = 2½ feet.5. Submodule:
one thirty-second of 2½ Carolingian inches
= 1¼ feet.
It should be noted that the value of the crossing square
(2½ Carolingian inches square) is developed from the value
of the next largest module (10 Carolingian inches square)
in the same manner in which the value of the small unit
(one sixteenth of 2½ Carolingian inches) is developed from
the crossing square: by the method of binary section.
All the surface calculations of the scheme are determined,
accordingly, by a geometrical ground relationship in which
each smaller base value is calculated as one sixteenth of the
superordinate value: the large module (40 feet square) is
one sixteenth of the super module (160 feet square), the
small module (2½ feet square) one sixteenth of the large
module (40 feet square).
In handling these modules, the designing architect displayed
an extraordinary sense of discretion, using each for
its specific purpose: the super module (160 feet square) for
the calculation of the overall relationship of the site, the
location of the axis of the Church, and the grouping of the
principal building masses (fig. 63); the large module (40
Claustrum (fig. 61); the small module for all dimensions
that were too small to be expressed by any of the larger
modules (figs. 59 and 60).
The Plan is drawn to a scale in which one foot on the
ground corresponds to one sixteenth of a Carolingian inch
on the parchment (which corresponds roughly to the
metric scale of 1:200), a ratio that one would consider even
today ideal for a plan of this kind, as it allows for easy
readability of details without obscuring primary values.
Figure 66A-D shows all of these relationships coordi-
of the yardstick of 40 Carolingian linear inches,
which we presume the drafter of the Plan used in designing
the scheme. See also Diagrams I, II, pages 92 and 93, above.
Kutsch, I, 1928, 94ff; Schmidt, 1932, 32ff; Behn, 1934, passim.;
Hanftmann, 1930, 229ff; Arens, 1938, 41ff; Rave, 1957, 52ff; Doppelfeld,
1948, 12.
"Item dicitur in Tungris pes Druhianus, qui habet monetalem pedem et
sescunciam." Hyginus, De Limitibus constituendis, ed. W. Goes (Amsterdam,
1674), 210.
Thus according to Sir William M. Flinders Petrie, in his article
"Weights and Measures, Ancient," Encyclopaedia Britannica, XXIII,
London, 1967, 378: "It connects with the base of the English land
measure . . . was the commonest building foot in medieval England (13.2
inches). It was also the basis for French architecture, the canne (of 78.24
inches) or six feet of 13.04 inches."
I.14.5
PURPOSEFUL MODIFICATIONS
One of the remarkable qualities of the planner of the
scheme of St. Gall is that, although he exhibits an extraordinary
sense of sophistication in the working out of
modular relationships, he does not hesitate to modify his
schematism when special conditions so require. I have
already alluded to this fact in my discussion of the 40-foot
module. There are two deviations from the use of this
module, which call for an explanation.
One of these is that accurate measurement of the aisles
of the Church shows them to be not 20 feet wide as their
explanatory title requests (latitudo utriusque porticus pedum
xx) but 22½ feet; the other is that the Dormitory and the
Refectory extend in places as much as 5 feet southward
over the 40-foot grid of the Claustrum (figs. 61 and 62).
What caused these modular incongruities? Are they due
to the carelessness of the copyist? Or are they purposeful
modifications? The latter possibility was suggested by
Arens, the former by Poeschel. Arens thought that the
surplus in the width of each aisle owed its existence to the
draftsman's desire to provide enough space for the thickness
of the walls of the church.[376]
Poeschel contends that
since the draftsman makes no concessions to the thickness
of the walls at any other place, it would be illogical to
expect him to do so here.[377]
Although Poeschel's argument is not to be dismissed
lightly, I am inclined to agree with Arens. We cannot infer
from the fact that the drafter of the Plan rendered the walls
of his buildings as simple lines that he was unaware of the
difficulties that might arise from this method of rendering
the more congested areas of the Plan unless they were forestalled
by special provisions from the very start. In the case

68. PLAN OF ST. GALL
A comparison of this with the preceding figure shows
how the draftsman, in developing his final version of
the plan of the Church, modified the square schematism
of the original concept—in which the aisles (PEDUM
XX) were assigned a width of exactly one half of the
width of the nave—by moving the aisle walls one 2½foot
module further outward. An instrument-drawn
grid of auxiliary lines, similar to the one above, enabled
the architect to plot the bases of nave columns, as well
as the location of altars and all other Church furnishings
with a precision so great that their exact
dimensional values were not lost in the freehand tracing
to which the Plan of St. Gall owes its existence.
The lines of the Plan as drawn on the parchment vary
considerably in width from less than 1/32 to over 1/16
of an inch, representing, at the scale of the document,
less than 6 inches to more than a foot. These widths do
not relate in any way to actual wall thicknesses. The
draftsman had a clear notion of line in the abstract
Euclidean sense of defining the limits of an area. The
lines comprise a diagram drawn to scale with astonishing
accuracy. As an instrument of communication it transmits,
at this scale and at this stage in the evolution of
the Plan, all that can be expected of any plan at this stage.
It is a graphic image delivering a message concerned
with policy and concept. Wall thicknesses of structures
as they might take shape in the future were irrelevant in
mind of the drafter and to the purpose. Quite possibly
he did have some vague notion that certain structures or
parts of them might be of masonry, wood, or metal,
according to the traditions of the time. Uppermost in his
thoughts was the message.
In viewing the purpose of the Plan in this light, as a
paradigmatic delineation of Benedictine planning policy
for a "model" monastic establishment, the Plan stands
on its own, without embroidery of detail that would come
with development by others for a particular site.
The Plan is capable of interpretation in more than one
way, and that was part of its intent. If the Plan is
interpreted today, in this way, or that way, we are doing
no different than what was intended. It is this capacity
of the Plan to stir the imagination almost 13 centuries
after it was drawn in the Scriptorium at Reichenau that
is among its remarkable characteristics, a property
common to all great works of art.
E.B.
STEP 2: CONCEPTUAL GROWTH OF THE LAYOUT OF THE
MONASTERY CHURCH

posed no problems as the space required for the wall
thicknesses in subsequent construction could easily be
borrowed from the open yard surrounding the building,
and did not have to be subtracted from the building itself.
But where a group of major masonry buildings butted
against each other, as in the case of the Church and the
adjacent claustral structures (fig. 61), the problem was
serious. Here the builder would have been forced to
borrow the space that he needed for the masonry either
from the interior of the Church or from the contiguous
gallery of the cloister, where spatial congestion was undesirable,
since this gallery, besides serving as a passageway,
was used for the daily assembly of the monks in
chapter. To obviate these contingencies the designer introduced
two safety measures: first, by increasing the width
of the aisles of the Church from 20 to 22½ feet; second, by
enlarging the contiguous cloister walk from 12½ feet (the
width of the other three wings of the Cloister) to 15 feet.
Without changing his style of rendering he thus interposed
a safety area 5 feet wide along the crucial line of encounter
of Church and Claustrum. He left it to the builder to
determine precisely what the thickness of the walls should
be but freed him from the need of invading any of the
adjacent spaces with his masonry as the building went up.
It is obvious that the insertion of this safety margin
between the Church and Claustrum would affect the layout
of the latter as well as its relation to the square grid. Thus
the cloister yard, instead of measuring 100 × 100 feet,
covers a surface area of 100 × 102½ feet; the Dormitory,
instead of measuring 40 × 80 feet, as one would expect in
the light of the 40-foot module, measures 40 × 85 feet;
in consequence all the buildings lying at the southern edge
of the claustral grid extend 5 feet beyond the southern
boundary of that grid.
On the north side of the Church it was equally undesirable
that any usable space be sacrificed to wall construction.
Here, too, the required space would have had to be subtracted
from either the Church or the contiguous Lodgings
for the Visiting Monks, the Master of the Outer School, and
the Porter.
I.14.6
SUCCESSIVE STAGES IN THE
CONCEPTUAL GROWTH OF THE
LAYOUT OF CHURCH AND CLAUSTRUM
If the observations on the modular basis of the Plan
presented in the preceding paragraphs of this chapter are
correct, the procedure followed in the construction of the
layout of the Church and the Claustrum can be reconstructed
as follows:
Step 1 (fig. 67):
The draftsman first constructed the grid of 40-foot squares
which determined the overall dimensions of the Church.
This grid established the boundaries of the nave, the
transept, and the choir, as well as those of the two subsidiary
contiguous spaces of the Sacristy and the Scriptorium.
The transept was composed of three, the nave of
four and one-half 40-foot squares. The introduction of an
extra half-square in the nave was inevitable, if the draftsman
started from the premise that his church should be
300 feet long. The columns of the nave arcades were
plotted at a distance of 20 feet, so that each second column
came to coincide with one of the corners of its corresponding
40-foot square. The width of the aisles, at that
stage, was meant to be half the width of the nave, i.e., 20
feet.
Step 2 (fig. 68):
In working on the internal layout of the Church, the draftsman
was aware that an acute shortage of space would occur
in actual construction if no allowance was made for the
thickness of the aisle walls where the Church was abutted
by other masonry structures. He took account of this
contingency by moving the center line of his aisle walls 2½
feet further out and producing the safety strip previously
mentioned. Within the schematic floor space of the church
created in this manner, he could now map out the foundations
for his columns and altars by a system of auxiliary
construction lines which divided the Church lengthwise in
the sequence
5 · 15 · 5 · 15 · 5 · 15 · 5 · 15 · 5 · 15 · 5 · 15 · 5 · 15 · 5 · 15 · 5 · 15
and crosswise in the sequence
5 · 5 · 7½ · 5 · 5 · 12½ · 10 · 12½ · 5 · 5 · 7½ · 5 · 5
The altar screens in the aisles are inscribed into 7½-foot
squares, the altars in the nave, the ambo, and the baptismal
font into 10-foot squares. The system of auxiliary construction
lines shown in figure 68 is the minimum required
for the internal layout of the Church.
Had the wall thickness been inked in as solid bars, the
Church would have appeared as shown in figure 56. This
is the manner in which it was interpreted by Graf, Ostendorf,
and Gall, and it is interesting to note that this concept
can be translated into the language of a modern architectural
drawing without sustaining the slightest distortion. Had the
designer of the Church intended to draw the Plan in this
manner, it would have been fully within the scope of his
capabilities. If he confined himself to the more abstract
procedure of simple linear definition, it probably was
because he had the task of designing the layout of not just a
church, but an entire monastery comprised of a multitude
of buildings of greatly varying dimensions, where the
drawing out of wall thicknesses would have introduced
unnecessary complications.
Step 3 (fig. 69):
After the floor plans of the Church were completed, the
draftsman could lay out the cloister yard with a relatively
simple system of auxiliary lines, inheriting from the

69. PLAN OF ST. GALL
STEP 3: CONSTRUCTION OF CLOISTER YARD. METHOD USED IN DEVELOPING LAYOUT OF YARDS AND WALKS
Our analysis of the cloister yard reveals an intense preoccupation not only with the mystique of the square, but also with sacred numbers 3, 4, 10, 40 (see
pp. 118-25). The cloister yard is inscribed in a 100-foot square within which is inscribed a 75-foot square, which in turn accommodates in its center a
20-foot square. The sides of each are respectively, 40, 30, and 10 standard 2½-foot modules. The porch arches, arranged in groups of 4, are each inscribed
in a 5-foot square (area: 4 standard modules); the passages between them into rectangles 4 modules wide and 3 high.

superordinate grid of 40-foot squares which transmitted
itself to all of the contiguous structures (Dormitory,
Refectory, and Cellar). The cloister yard was designed to
cover a surface area 100 feet square, and as a strip 12½ feet
wide was taken off on either side for the covered walk (15
feet in the north), a surface area 75 feet square was left for
the open pratellum in the center. Arches which open into
the latter from the center of each covered walk are 10 feet
wide and 7½ feet high, while the galleried openings on
either side measure 5 × 5 feet, leaving in the corners a
solid piece of masonry 7½ feet long. The square in the
center of the pratellum measures 20 feet on each side.
I.14.7
DIFFICULT OR INSOLUBLE FEATURES
Although the Plan of St. Gall reflects the original scheme
with an amazing accuracy, the irregularities that slipped
into the design as it was traced through the opaque body
of the sheets of parchment created a number of problems
that are hard to settle and may have to remain unsolved.
Foremost among these are certain aspects in the layout of
the Cellar, the Scriptorium, and the Medicinal Garden.
THE CELLAR
In contrast to the Dormitory and the Refectory, to which
it corresponds in all other respects, the great monastic
Cellar, which lies on the western side of the cloister yard,
is not 40 feet wide, but has a width that ranges somewhere
between 35 and 37½ feet (fig. 70.A-C). The building is
firmly drawn except for its western long wall, which swerves
inward and is a little more shaky than the draftsman's
average line. Its curve runs parallel to a seam that fastens
two sheets of parchment and it looks as though its wriggling
and swerving course owed its existence to the copyist's
desire to avoid this seam. Had the copyist drawn the western
long wall at the exact distance of 40 feet from the opposite
wall, he would have had to superimpose the line that
defines the course of that wall on the seam for a considerable
distance, running his quill over the projecting loops
of the thread. It appears probable to me that it was the
wish to avoid this complication that pushed the line of the
western long wall of the Cellar further inward. By how
much he displaced this line, the draftsman could not even
judge at this point, as the overlapping edges of the two
connecting sheets of parchment which separated him from
the original prevented him from actually seeing the corresponding
line of the prototype plan.
The layout of the remaining portions of the Cellar
presents no problem. The dimensions of the barrels, both
small and large, as well as of all the interstices between
them, are multiples of the 2½-foot module (fig. 70.C). The
small barrels are 10 feet long and have a central diameter
of 5 feet. Their outside curvatures are struck with a radius
of 12½ feet. The large barrels are 15 feet long and have a
central diameter of 10 feet. Their stave curvatures are
struck with a radius of 15 feet. The rails on which the small
barrels rest are 5 feet apart. The distance between the
rails of the large barrels is 7½ feet.
SCRIPTORIUM & NORTHERN TRANSEPT ARM
An irregularity which, I confess, I cannot solve, is found
in the dimensions of the northern transept arm and of the
adjacent Scriptorium (fig. 61). Both of these spaces
should be 40 feet square, but are slightly less. In order to
be 40 feet square the head wall of the northern transept and
the adjoining wall of the Scriptorium would have had to
project by 2½ feet beyond the line of the outer wall of the
Rooms for the Visiting Monks, which abut the northern
aisle of the Church. Yet the Plan does not show such a
projection. Is this through error of the copyist? Or was it
a purposeful modification undertaken by the drafter of the
prototype plan? I am inclined to assume the former, as
only a 40-foot square would provide for a symmetrical
layout of the transept and a consistent arrangement in the
windows and writing desks along the northern and eastern
wall of the Scriptorium. However, one cannot be sure of
this. In general, the designer strove for symmetry, but to
contend that he did so without exception is a different
matter.
THE MEDICINAL GARDEN
A third case difficult to settle is the apparent displacement
of the Medicinal Garden (fig. 62). It lies in the northeastern
corner of the monastery site, but is out of line with
the protruding outhouses and hypocaust flues of the
Novitiate and the Infirmary. It was the last installation to
be drawn on the sheet containing all the buildings lying
to the east of the Church. I can explain its peculiar position
only by the assumption that the copyist lost space through
an accumulation of small irregularities, as he drew the last
row of buildings near the right-hand edge of sheet 4 in the
sequence, House for Bloodletting, House of the Physicians,
Medicinal Garden.
THE HOUSES FOR THE COWS AND THE
FOALING MARES
The dimensions of the houses for the cows and the foaling
mares can only be guessed at, as the narrowing of the
parchment at the southwestern corner of the monastery
forced the copyist to decrease the size of these two houses
along the southern edge of the monastery site (above,
p. 48f.; figs. 483 and 487). To what extent it is impossible
to say.
I.14.8
CONCLUSIONS
The foregoing analysis of the construction methods employed
in the Plan of St. Gall should dispel, once and for
all, the widespread belief that medieval architectural drawings
were not made "to scale."[379]
In contradiction to traditionally

70. PLAN OF ST. GALL. MONKS' CELLAR
The swerving uncertain ductus of
the line which defines the position
of the western long wall of the
Cellar (inconsistent with the
firmness of the drawing elsewhere
in the Plan), as well as departure
from the correct position of this
line (not 40 but 35-37 1/2 feet
distant from the opposite wall) is
conditioned, in our opinion, by two
factors:
1. This line is drawn where the
overlapping margins of two
connecting sheets of parchment
(sheets 1 and 2; cf. above, pp.
35-37 and p. 34, Fig. 24.A)
which, because of their thickness,
made it impossible for the draftsman
to see the corresponding lines of the
prototype plan as he traced it; and
because
2. the draftsman tried to avoid the
stitching by which the two sheets
were sewn together (shown in grey
tint within the margin of the
parchment) and which his quill
would have had to straddle had he
drawn the line at its proper
geometrical position.
(Cf. fig. 235, p. 286, and caption.)
A. Facsimile reproduction of the red drawing of the Plan (see caption, page 13, vol. III)
B. Same with 2½-foot module grid superimposed
C. Possible scheme by which the layout shown in A was constructed

observations made by Boeckelmann and Arens—this
analysis demonstrates that the author of the original scheme
of the Plan availed himself not only of a clearly definable
scale, but that he applied this scale throughout the entire
layout of the Plan with full consistency and logic.
From the methods employed in modern scale construction
the Plan of St. Gall differs neither in the logic of its
graduations, nor in the truthfulness with which this
graduation reflects the variations of the rendered object.
From the methods of modern scale construction the Plan
of St. Gall differs in two points only: first, in the fact that
it flows from a basically modular type of thinking; and
second, that its basic working units are derived as fractions
or multiples from a dimensional master value.
If a modern architect assigns to a given area a value of
40 feet, he does so with the aid of a ruler, on which the
value 40 is graduated into forty equal parts of one. On the
scale of the Plan of St. Gall, quite differently, the magnitude
40, as is found, was not subdivided into forty units of one,
but into sixteen units of 2½. Why the author of the Plan of
St. Gall divided his 40-foot scale into 16 units of 2½ rather
than into 40 units of one must by necessity remain a matter
for speculation. The value 2½, as my colleague Hunter
Dupree points out to me, was a fundamental unit of the
English surveying system. Two and one-half feet is the
length of the English pace (the space traversed by one
step).[380]
Could it be that the 2½-foot standard module of the
Plan of St. Gall was the equivalent of a traditional and
widely used Carolingian pace? And that the superordinate
modules of 40- and 160-foot squares were calculated as
meaningful multiples of that pace? There are other
historical factors which may have contributed to the
genesis of such relationships. To subdivide a primary value
of 40 into sixteen equal fractions (or to arrive at that value
by multiplying sixteen times a primary value of 2½) as has
been pointed out on the preceding pages, is one of the
easiest and, for that reason, also the oldest operations of
the human mind, requiring no other instrument than a
straightedge and a compass (method of continuous halving
or doubling). In chosing this procedure, the draftsman may
also have been influenced by the eminently sacred connotations
associated in his day with the two basic figures used
in this operation, the figures 40 and 4.
The choice of the figure 40 for the width of the nave can
hardly be considered an accident. Forty was a number
which in Biblical tradition had been associated for ages
with periods of expectation and penitence. Forty were the
days of the great primeval deluge, forty the years that the
Hebrews spent in the desert, forty the days that Moses
passed in expectation on Mount Sinai, forty the days
announced by Jonah for the destruction of the city of
Nineveh, forty the days that separated the Ascension from
the Resurrection.[381]
Forty, it should be noted, is not only
the width attributed on the Plan of St. Gall to the nave and
the transept, but also the total number of buildings of
which the monastery is composed.
In halving this sacred figure four times in succession, the
draftsman put into operation another eminently sacred
figure, associated both in the pagan and the Christian
tradition with the basic divisions of matter, time, and
space: the four elements, the four seasons, the four rivers
of Paradise, the four cardinal virtues, the four main
prophets, the four evangelists.
Whatever his reasons may have been (and I shall say
more about the number symbolism of the Plan a little later)
which all values could be expressed as multiples of 40 or as
multiples of a fraction obtained by halving 40 four times,
the draftsman provided his plan with a scale that could be
read and applied by anybody who was familiar with the
principles involved or who knew the formula. It is due to
the relative largeness of its standard unit (2½ feet) that the
Plan owes its easy readability, and that it could be traced
upon another sheet of parchment without sustaining any
serious loss in clarity and measurability.
The development of a modular grid in which all superand
subordinate units are derived in logical steps of progression
or diminution from the dimensions of a controlling

highest order and a concept that was tragically corrupted
when—(I presume at the second synod of Aachen, as the
Plan was formally considered for adoption[383] )—it was decided
that the length of the church should be reduced from
300 feet (as shown in the drawing) to 200 feet (as stipulated
in the axial title of the church) and that the interstices of
the arcades should be reduced from 20 feet (as shown in
the drawing) to 12 feet (as stipulated in the title inscribed
into the arcades). Like the number 40, the number 12
belongs to a traditional repertoire of sacred figures that
formed a common currency of metaphor and analogy (the
twelve Judaic tribes, the twelve apostles, the twelve months
of the year, the twelve hours of the day, et cetera),[384] that
could be put into circulation on even the most precipitate
call. But in contrast to 40, 12 as a dimension is not part of
the modular grid of the Plan. Being neither a multiple nor
a fraction of 40, it is clearly a foreign body in this system.
In introducing this figure for a feature aesthetically as
prominent as the arcades of the nave, the churchmen who
prescribed this change demolished one of the most precious
and most innovative aspects of the Plan: its square schematism.
It is probable that we will never be able to establish
who they were, these men,[385] yet one thing is certain: they
could not, in any manner, have been involved in the design
process that went into the making of the original scheme—
and they were worlds removed from understanding its
unusual aesthetic merits. To shorten the church by 100 feet
did not in itself require abandoning the modular scheme.
It could have been done in increments of its own control
module by the simple elimination of five 20-foot bays in
the nave. But the stipulation that the interstices of the
arcades be reduced from 20 to 12 feet forestalled any such
possibility and effectively destroyed the system of squares
in the church. The change was drastic, and, had it been
implemented in the drawing, would have required the
preparation of an entirely new Plan.
We are faced here with a manifestation of the age-old
conflict between architectural creativity and administrative
control, with disastrous consequences for the former when
the latter unwittingly becomes involved in the design process
with decisions which, though not necessarily arbitrary,
are nevertheless extraneous to the creative act and innocent
of any knowledge of technical detail and planning.
The author of the original scheme, if he was present at
the gathering where these decisions were taken, must
have gone through moments of shattering pain. He had
produced a scheme of extraordinary conceptual subtleties
including the design of a church which, had it ever been
built, would have been one of the highlights of early
medieval architecture (fig. 110). It took two-and-one-half
centuries of further development in western architecture
before the ideas first conceived here were embodied in some
of the great Romanesque cathedrals of Europe.[386]
On the English pace of 2½ feet (the distance measured from the heel
of one foot to the heel of the other as it touched the ground in walking),
see Murray, op. cit., sub verbo. The Roman pace (passus) was twice the
length of the English pace, that is, five feet (the distance measured from
the heel of one foot to the heel of the same foot when it touched the
ground again). The Roman pace was internally divided into two gradus
of 2½ which may have been the prototype of the medieval English pace.
Gradus, in Classical Latin, is used both as a designation for a step taken
in walking and as a designation for a step forming a tread or rung of a
stair or ladder. On the Plan of St. Gall it appears in connection with
seven steps (septum gradus) which lead from the crossing to the fore choir.
It is amusing to note that their tread had a standard value of 2½ feet. See
above, p. 89. (On the Roman passus, see Hultsch, 1862, 65ff and 1882,
79f). Attention should be drawn in this connection to the fact that in the
elevations of at least two outstanding Carolingian buildings, the Palace
Chapel at Aachen and the Gate House of the Abbey of Lorsch, the 2½
foot module is systematically used as a unit of measure (see Arens, 1938,
47 and 75 and for later examples, ibid., 95, 106 and 107; for more incidental
use of the 2½ foot module see ibid., 14, 19, 27, 30, 32, and
43). Since these lines were written Hunter Dupree has deepened our
knowledge on these relationships as well as their connection with later
measuring systems in two illuminating studies, a summary of which will
be found in Appendix III, Vol. III.
On the sacredness of the number 40 see Roscher, 1909, 105ff; and
Encyclopedia Cattolica, VII, 1952, col. 1996; Enciclopedia Italiana, XXV,
1935, 38; and Ursula Grossmann, 1954, 4-41.
The biblical associations connected with the number 40 were so
powerful as even to suggest a division of the hour into 40 moments. Bede,
as Charles W. Jones points out to me, makes mention of both, a division
of the hour into 40 and into 60 moments; but in a commentary to Bede's
De temporibus ratione, perhaps written by Henri of Auxerre and quoted
in several ninth-century manuscripts, the statement is made that the
hour is divided into 40 moments: si vis partyri horam in ·xl· vel diem vel
aliquid huiusmodi ipsa xl pars momenti nomen accepit, seniis xx, x momenta
quadrans, xxx dodrans. (Jones, 1939, 98 (701-702).)
For other manifestations of number symbolism on the Plan of St.
Gall see the chapter "Numeri Sacri" below, pp. 18ff.
For more details on this hypothesis see the chapter Reflections about
the Prototype Plan, and in particular pp. 29ff.
For a fuller discussion of the problems touched upon here see the
chapter on numeri sacri, below, pp. 118ff.
In Fulda it was the monks who first asked for restraint in the construction
of a church which they considered to be "of inordinate size"
and petitioned that the Abbot be directed to reduce the building program
to normal proportions. The grievance was submitted to Charlemagne in
A.D. 812 but fell on deaf ears. In 817 however the climate had changed
and it became the leaders of the church who espoused this view and in
implementing it deposed the abbot (see below, pp. 187ff).
I.14.9
CONFIRMING EVIDENCE:
THE PALACE GROUNDS AT AACHEN
We do not know whether or to what extent, if ever, the
modular construction methods used on the Plan of St. Gall
were implemented in any of the larger monasteries built or
rebuilt during the reign of Louis the Pious. But one other
site, a physical and historical reality, can be said to have
been organized along similar lines: Charlemagne's Palace
at Aachen. While Ernest Born and I were working on the
Plan of St. Gall, Leo Hugot of Aachen made a meticulous
dimensional survey of the palace grounds and its buildings.
None knew of the other's work, which was simultaneously
and for the first time displayed in 1965 at the Council of
Europe Exhibition Karl der Grosse in Aachen, each in the
form of a model, together with two brief explanatory statements
that formed part of the official Exhibition Catalogue.[387]
Charlemagne's Palace at Aachen was established on the
ground of an old Roman settlement that—like most other
Roman provincial towns or military camps—was inscribed
into a large rectangle, internally divided into four equal
quarters by two streets intersecting each other at right
angles, conditions that are even today mirrored in the
course of certain streets of the city of Aachen (fig. 71.X).
In the southeast corner of that rectangle were the famous
hot springs, the amenities of which were one of the primary
reasons for the selection of this site as the first "permanent"
residence of the great ruler. In laying out his residence,
Charlemagne did not follow the Roman dispositions
blindly. He changed the alignment of his buildings so that
the axis of the Palace Chapel would run from west to east,
as the liturgy demanded, and since all of the other buildings
of the Palace were either parallel or at right angles to the
church, this system of building came to lie athwart, at an
angle of 38 degrees, the Roman street system. As the
Romans had done with their settlement, so Charlemagne
also inscribed his residence and its buildings into an area
of rectangular shape (fig. 71.Y). In laying out his grounds
he availed himself, as the dimensional survey of the site by
Leo Hugot shows, of a modular base value consisting of a
rod 12 feet long. He placed the Palace Chapel (fig. 71.Y, 1)
against the southern edge, the Audience Hall (fig. 71.Y, 5)
against the northern edge of a large open square, each side
of which had a length of 30 rods = 360 feet. Internally
this square was composed of 16 smaller modules, each of
which formed an equilateral square of 7 rods = 84 feet.
The Palace grounds were intersected by two streets which
crossed each other at right angles dividing the site into an
outer and an inner court. These streets were each 2 rods
broad = 24 feet, bringing each side of the square to a total
of 30 rods = 360 feet. Hugot's analysis of the square grid
of the Palace grounds (Hugot, 1965, fig. 2 facing p. 524)

(fig. 71.Y, 5) or the site of the southern annex to the Palace
Chapel; the so-called Secretarium (fig. 71.Y, 4). Ernest
Born's analysis, superimposed in red on Hugot's plan
shows that with these two buildings included, the whole of
the Palace grounds could be conceived as being inscribed
into a rectangle, measuring 30 rods in width (30 × 12 =
360 feet) and 52 rods in length (52 × 12 = 624 feet). He
emphasizes in his caption to fig. 71.Y the importance of the
use of the sacred numbers 3, 4, 10, 12, 30 and 40 in the
construction of this grid.
The proportions of the Palace Chapel, Hugot's analysis
has shown, were as carefully and consistently regulated as
the layout of the entire Palace grounds (figs. 71.Za, b, c).
The base module, again, is a rod 12 feet long. The chapel
itself was fitted into a square, each side of which measured
84 feet = 7 rods (fig. 71.Za). To this cube was added in the
east a choir 24 feet deep (2 rods), and on the entrance side
a westwork of identical depth. In the vertical plane the
84-foot cube reaches from ground floor to base of the
pyramid. The total elevation is composed of: height of
outer wall, 48 feet (4 rods); height of gallery roof, 12 feet
(1 rod); height of drum, 24 feet (2 rods).
The height of the pyramidal roof of the octagon, in this
context (the original pyramid has disappeared) can only
have measured 2 rods = 24 feet. The total height from the
ground to the apex of the structure, accordingly would be
9 rods = 108 feet.
This is not the time to go into the structural aesthetics of
this important building.[388]
But I cannot forego the pleasure
of remarking on the implications Hugot's findings had with
regard to our own work. First of all, it removed whatever
residual doubt Ernest Born and I may still have entertained
concerning the correctness of our interpretation of the Plan
of St. Gall. Second, it added new weight to the arguments
which we have advanced in a preceding chapter concerning
the provenance of the original scheme from sources close
to the Court School as well as to Bishop Hildebold, the
titular head of that school (791-819).
Bishop Hildebold's church at Cologne, as has been shown
in a preceding chapter, served as model for the Church of
the Plan of St. Gall.[389]
The site organization methods, which
Leo Hugot has shown were used for the Palace of Aachen,
are greatly akin in spirit to those which we have shown to
have been used in the layout of the Plan of St. Gall. This
kinship suggests that the designer of the latter was not only
familiar with, but in all likelihood inspired by the former.
He might even have had access to the original drawings
used for the Palace grounds and its buildings.
The importance of Leo Hugot's findings about the
modular construction methods used in the layout of
Charlemagne's Palace at Aachen can hardly be overemphasized.
It is here for the first time in the history of
medieval (and possibly Western) architecture and site
organization that not only the grounds, but also the most
important building on these grounds, the Palace Chapel,
are controlled by a binding and all-pervasive rule of modular
prime relationships. We shall return to this problem
later on in a discussion of the possible historical roots of
this concept.[390]
AACHEN, PALACE CHAPEL. TRIBUNE
DETAIL, BRONZE RAILING, CA. 800
Eight such railings, each 4 feet high and nearly 14 feet long, were each cast in one piece:
an astonishing accomplishment of the Carolingian Renaissance. Roman grille work patterns,
Byzantine acanthus leaves, and Hiberno-Saxon scroll-and-grid motifs are subsumed in
a sophisticated medieval linearism.

71.X AACHEN: THE CITY CENTER. A CADASTRAL PLAN AFTER 1800 WITH
CHARLEMAGNE'S PALACE GROUNDS
Superimposed in red are the grounds and buildings of Charlemagne's Palace as well as the reconstructed street
system of the Roman town of Aquae Granis (redrawn in part by Ernest Born, after Hugot, 1965, fig. 1 facing
p. 534, and with the aid of Hugot's original drawing which he generously made available to us for that
purpose).
Like most Roman towns or military camps this settlement was internally divided into four quarters by two
main arterials intersecting each other at right angles. The course of these, as Leo Hugot has shown, are
recognizable in the street alignment of the modern city of Aachen. They are: from north to south, the
alignment Kockerell Strasse—Klostergasse and Kleine Marschier Strasse (A-B); from west to east, the
alignment Jakob Strasse and Grosse Koln-Strasse (C-D). The latter was part of a Roman road that led from
Herleen to Kornelismünster into the Eifel Mountains; the former of a road that connected Liège with Julich
and Cologne.
The city of Aachen (French: Aix-la-Chapelle; Italian: Aquisgrana) owes its name to a Celtic settlement and
sanctuary that had sprung up in the vicinity of a cluster of sulphur hot springs which the Romans after their
conquest of this territory, in the first century A.D. converted into a watering place for legionaries, pensioners,
and other civilians visiting or settling there for recreational purposes or for reasons of health. The Romans
referred to this location as Aquae Granis = "the Waters of Granus" (a Celtic deity worshipped in connection
with hot springs). In ancient times, as well as in the Middle Ages and up to our own days, this kind of spring
was believed to have a curative effect on such afflictions as gout, arthritis and scrofula.
At the collapse of the Roman empire the city of Aquae Granis was destroyed (presumably around 375) but the
life of the native population appears to have continued. King Pepin bathed in the springs of Aachen in 765
and ordered the baths to be cleaned. Charlemagne signed deeds in AQUIS PALATIO PUBLICO in 768 and 769,
and between 777 and 786 rebuilt and enlarged his father's palace. The site became his favourite winter
residence from 794 onwards, a date which marks the turning point from ambulant government to rule from a
central seat of government, at least during the winter months, the summers continuing to be taken up by
warfare. Charlemagne furnished the site with a royal Audience Hall and a monumental Palace Chapel (fig.
71.Z), a residence for himself (location and details of construction unknown) as well as a considerable number
of lesser buildings to house his court as well as his bodyguards.
The Palace, as was to be expected, gave rise to the growth of a vast cluster of subsidiary establishments,
mainly to the north and to the west of the royal court, and acquired the appearance of the town when all of
these VICI, together with the Palace, were surrounded in 1172-1176 with a wall by order of Emperor Frederic
Barbarossa.


71.Y SITE PLAN OF THE EMPEROR'S AUDIENCE HALL AND THE PALACE CHAPEL AT AACHEN,
BUILT BETWEEN 796 and 804
KEY TO NUMBERS OF PLAN
1. THE PALACE CHAPEL
2. ATRIUM
3. NORTHERN ANNEX
Metatorium where the emperor changed his attire before entering the chapel
4. SOUTHERN ANNEX
Secretarium for assembly of the clergy and the holding of synods in contemporary sources referred to as In Laterano
5. THE EMPEROR'S AUDIENCE HALL
6. ENTRANCE HALL at ground level connects the OUTER COURT with the INNER COURT
7. BARRACKS for the emperor's guard
Superimposed on Hugot's drawing of a part of the Emperor's Palace at Aachen is shown the rectangular schematism on which its plan is
based. The basic module, as Hugot's dimensional survey of the site has demonstrated, measures 12 feet. Seven basic modules comprise one
major unit. The length of the plan is 7 major units, plus 2 basic modules for the east-west street, plus 1 basic unit for the projection of the
north apse of the Emperor's Audience Hall. Thus the length of the rectangle is 7 × 7 plus 3 units, or 52 units; its width is 4 × 7 units plus
2 units, or 30 units—a rectangle 624 feet long by 360 feet wide.
What captures our attention is the prevailing scheme of numerical and space relationships. The sacred numbers 3, 4, and 7, with 10, 12,
and 40, represent values of measurement that govern or control lines and critical grid relationships and are suffused into the fabric of the
plan to form interrelated kinships. For example, the length of the plan, 52 units, saturated with 75 [(7 × 7) + 3] is the sum of 40 plus 12.
The width of the plan, 30 units, is the product of 3 × 10 and, with 12 as a multiplier, creates 360 feet [(3 + 3 + 3) × 40]. Such a collection
of NUMERI SACRI offers striking evidence of the presence of sacred numbers as a dominating influence in the mind of the Carolingian
planner at the heart of the Empire, at this period in the development of western civilization. The aesthetic consequences of this pervasive
geometric and numerical schematism is another and different problem. Too, it is not without interest that the 3-4-5 triangular relationship
for the formation of a right angle is consonant with the 12-foot grid and would facilitate, in the field, layout for building foundations. In
monumental building schemes in particular, and all building in general, this would be advantageous to both the architect and his director
and construction foreman on the site.
Thus, rectangular schematism, identifiable with esoteric sacred numbers, was well-tailored in some respects to the practical needs of a
builder whose responsibilities, far removed from finely woven webs of theology, were characterized by mundane objectives, intolerant of
hocus-pocus.
E. B.


71.Za AACHEN, PALACE CHAPEL, BUILT BETWEEN 796 and 804
PLAN AND ELEVATIONS BY LEO HUGOT
GRID SUPERIMPOSED BY AUTHORS
The interesting and developmentally crucial significance of Leo Hugot's discovery of modular principles governing the organization of the Palace
Chapel at Aachen is its demonstration, by implication, that even a centrally planned Carolingian building cannot escape the power of
transformation which, at the age of Charlemagne, converts the Early Christian basilica into a modular structure.
The design of the Palace Chapel at Aachen is based on that of the church of San Vitale at Ravenna, begun around 532 and finished in 546.
In both buildings the shape and composition of the primary spaces as well as the formation of the basic morphological features are essentially the
same. In each case a tall octagonal center space with fenestrated and dome-surmounted drum is encircled by a peripheral envelope of outer
spaces, which, although internally divided into two stories (ambulatory and gallery) are, in their combined height, lower than the center space.
In each case the drum with its dome rests on eight huge arches, rising from piers erected in the eight angles of the octagon (cf. fig. 162.B).
These are the basic compositional and structural features. Yet in style and spatial concept the two buildings differ distinctly. In San Vitale the
shell separating the octagon from its spatial perimeter is made up of semicircular niches that billow out into the body of ambulatory and gallery.
Despite their intensive perforation (three arched openings on each level) these curved niches, together with the piers to which they are attached,
are aesthetically perceived as a continuous sheet of masonry stretched around the center space. The movement is encircling, not divisive, and the
enveloped space, being uninvaded by any of the enveloping features, retains its full corporeal solidity and homogeneity. It is sculpture springing
from a concept of spatial mass akin in spirit to the monolithic self-containment of the component spaces of the Early Christian basilica (Cf.
figs. 174 and 177.A-C).
The stylistic and conceptual archetype and prototype of this manner of molding space is the Roman Pantheon, a body of incomparable globular
perfection and beauty contained in a masonry shell of simple cylindrical shape whose surfaces pass in unbroken planar continuity into those of
the semicircular dome by which it is surmounted, with no intrusion at any point. The camera—one-eyed and stationary—is incapable of
capturing this quality of style, but Giovanni Piranesi, with his uncanny sensitivity for such matters, has portrayed it with great perspicuity in a
series of masterful engravings.
The design of the Palace Chapel at Aachen by contrast is based upon the concept of spatial divisibility. This quality is strikingly reflected in the
manner in which the eight component surfaces of the octagon meet and connect with one another. Instead of billowing niches swinging inward and
outward, yet never losing their encircling hold, the Chapel's straight surfaces, separated by sharp lines, rise in undisrupted ascent from the
ground to the apex of the vault by which it is covered. The dome over the octagon of San Vitale is circular (or nearly so) and therefore
detaches itself distinctly from the octagonal shape of the body of space lying beneath it, the transition from octagonal drum to circle of the dome
being achieved by means of squinches. It rests or hovers like a protective lid over the space it covers. The dome over the octagon of the Palace
Chapel, by contrast—a cloister vault, not a hemicycle!—is segmented into eight separate parts, like the eight sides of the octagonal shell that
supports it. The emphasis thus is shifted from connecting surfaces to separating lines. In Aachen, for this reason, the center space conveys the
feeling of being "sliced" or "sliceable" rather than "whole" and "rounded." It could aesthetically be defined as an aggregate of triangular
prisms, meeting with their sharp inner edges in the center axis of the building. This is divisive Carolingian modularity: the conceptual equivalent
of the modular square division of the Carolingian basilica (figs. 166-173); medieval divisionalism versus Classical corporeality.
The differences are discernible with even more striking sharpness in the structural articulation of the outer spaces. In San Vitale, ambulatory
and gallery were covered by timber roofs formed by continuous sequences of beams or trusses all lying on the same level, and therefore visually
perceived as flat and continuous annular planes (the present vaults are medieval; see Krautheimer, 1965, 170). In the Palace Chapel at Aachen
the same spaces are covered, on ground floor level by groin vaults of alternating square and triangular shape; and on gallery level, by rampant
barrel vaults alternating with sharply defined triangular spaces. This is cellular medieval organization of space, springing from the same
conceptual sources that in the longitudinal layout of the basilica lead to the arch-framed bay division of the Romanesque and the Gothic
(fig. 177); and for more visual demonstration, Horn and Born, Viator, 1975, figs. 38, 39.A-B.
Centrally planned buildings do not lend themselves with the same ease to modular division and, for that reason, are not part of the mainstream
of medieval development. One hundred and fifty years after the construction of the Palace Chapel, a sophisticated Florentine architect created in the
Baptistery of that city, a synthesis between classical and medieval, disclosing that even south of the Alps materials inherited from antiquity are
reshaped in a similar manner (cf. Horn, 1938, 99-155; reprinted 1973).

71.Zc FRONT ELEVATION
71.Zb SIDE ELEVATION
For the Plan of St. Gall, see Horn, 1965, 402-10 ("Das Modell eines
Karolingischen Idealkloster") and idem, 1965, 391-400 ("La Maquette
d'après le plan de St. Gall"). For the Palace grounds at Aachen, see
Hugot, ibid., 395-400 ("Die Pfalz Karls der Grossen in Aachen") and
385-390 ("Le palais de Charlemagne à Aix-la-Chapelle") as well as the
more detailed and more comprehensive analysis in Hugot, 1966, 534-72.
We acknowledge with profound gratitude Dr. Hugot's generosity in
allowing us to make use of his original drawings in the preparation of
the red overlays reproduced in figures 41.Y, 71.Y and 71.Za, b, c.
| The Plan of St. Gall | ||