|
Alternatives to Cumulative Sums
Studies in bibliography | ||
Alternatives to Cumulative Sums
Farringdon asserts but does not prove that her "language-habits" help to
distinguish one author from another. As I have already suggested, the assump-
tions behind her method may not have a reliable linguistic basis. But how
can
we know? One could test the hypothesis that Farringdon's
"language-habits"


FIGURE 8. Jill Farringdon's sample as scatterplot.
statistical techniques to do so that have nothing to do with cumulative sums.
Farringdon wants to explore the relationship between two variables: the num-
ber of total words per sentence and the number of words in a particular class per
sentence. To display this relationship, one would not use cumulative sum
charts
(which are not used to display the relationship between two
variables), but a scat-
terplot. The scatterplot would use the horizontal
axis for total number of words
per sentence, and the vertical axis for
number of words in a particular class per
sentence. For the following
example, I will use the same class that I have used
throughout, namely two-
and three-letter plus initial-vowel words. Each point on
the scatterplot
represents the data for a single sentence. The scatterplot also helps
to
avoid the problem of sequence that plagues QSUM, since the rearrangement
of
sentences in the sample will not change the appearance of the scatterplot.
Figure 8 is a scatterplot for Farringdon's 31-sentence sample.
One can immediately tell certain things about the relationship between the
two variables. First, one can see that longer sentences tend to have more two- and
three-letter plus initial-vowel words. (As I have already shown, this is not
in any
way a surprise.) Statisticians would call this a positive
association. The relation-
ship also seems to be linear, since the points
tend to cluster around an imaginary
line. Statisticians would also state
that this relationship seems to be particularly
strong, since the points lie
relatively close to this line with little "scatter."
Since the relationship appears linear, we could draw a line through these
points. Obviously, we would like to draw the best possible line, and the "least-
squares regression line" meets this demand in the sense of minimizing the
error in
predicting the number of two- and three-letter and initial-vowel
words. Figure 9
adds the regression line to the scatterplot in figure 8. A
commonly used quan-
titative measurement of how well the line fits the
points in the scatterplot is the
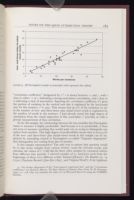

FIGURE 9. Jill Farringdon's sample as scatterplot (with regression line added).
close to either −1 or 1 indicating a strong association (correlation), and r close to
0 indicating a lack of association. Squaring the correlation coefficient (r 2) gives
the portion of variation in the vertical axis that is explained by the horizontal
axis. In this instance, r 2 is .905. That means that 90.5% of the variation we see
in the number of two- and three-letter plus initial-vowel words is explained by
the number of words in the sentence. I had already noted this high degree of
correlation from the visual inspection of this scatterplot; r 2 provides us with a
precise measurement of that correlation.
So for this sample, the relationship between the two variables that Farringdon
wants to measure is highly predictable. And because it is so predictable, it
does
not seem to measure anything that would assist one in trying to
distinguish one
author from another. This high degree of predictability
means that at most 9.5%
of the two- and
three-letter plus initial-vowel words in this sample can be ex-
plained by
something related to Farringdon's so-called "linguistic fingerprint"
that
distinguishes her writing from that of another.
Is this sample representative? The only way to answer that question would
be
to take many samples from various writers, count the relevant words, and
calculate the values of r
2. I did this for three other samples by canonical writers
from different time periods. I selected samples of 31 sentences each from
the
beginnings of these very different works: Samuel Johnson's The Rambler no. 14
(1750), Charlotte Brontë's
Jane Eyre (1847), and Virginia Woolf's To the Lighthouse

| Author | Average Words per Sentence ± Standard Deviation |
Average 23lw+ivw per Sentence ± Standard Deviation |
Ratio of 23lw+ivw to Total Number of Words per Sentence (slope of regression line) |
r 2 |
| Johnson | 49.6 ± 19.1 | 27.9 ± 11.8 | .58 | .889 |
| Brontë | 31.1 ± 23.2 | 15.4 ± 12.6 | .54 | .972 |
| Woolf | 37.9 ± 38.0 | 19.1 ± 19.4 | .51 | .985 |
| Johnson, Brontë, Woolf, and Farringdon combined (124 sentences total) |
35.2 ± 26.5 | 18.5 ± 14.5 | .54 | .959 |
(1927).[14]
Table 9 presents the compiled data for the samples from these three
works along with a combined dataset that contains all 124 sentences from John-
son, Brontë, Woolf, and Farringdon.
The high values for r
2 show that the primary and almost exclusive factor in
determining the number of two- and three-letter plus initial-vowel words is the
length of the sentence itself. In order to substantiate this point more
fully, one
would have to draw on many more samples. But the evidence I
present here is
quite suggestive. These three writers from three different
centuries have very dif-
ferent styles, as suggested by the very different
average lengths of their sentences.
Despite that important difference, the
similar values of r
2 show that for each of
these three samples, the
correlations between the two measured variables are
extremely strong.
The combined sample of sentences from Johnson, Brontë, Woolf, and Far-
ringdon is even more suggestive. The value of r
2 is again quite high. If one
were to remove sentences
by Johnson from this combined sample, the strength
of the correlation would
not significantly change. The average sentence length
would change, since of
these four writers, Johnson's average sentence length is
the greatest. (Any
casual reader of Johnson's essays knows that his sentences tend
to be
relatively long.) However, the "language-habit" under discussion does not
refer to sentence length by itself, but to the relationship between sentence
length
and two- and three-letter plus initial-vowel words. The information
in table 9
suggests that that relationship (as measured by r
2) will not vary significantly no
matter how many
sentences are removed from the combined sample and re-
gardless of the
authorship of those sentences. At least for these samples, this
"language-habit" fails to distinguish these authors from one another, and a
quantitatively-based attribution method that fails to distinguish between the
writ-

is of no value.
Based on this admittedly limited amount of evidence, I would hypothesize
that the relationship between sentence length and the number of two- and three-
letter plus initial-vowel words is highly predictable, and perhaps
universally so
for non-technical writing in the English language in the
modern period. That
hypothesis is supported by the remarkably similar ratios
between this category
of words and the total number of words for all these
samples. If my hypothesis
is correct, then the relationship is so
predictable that it does not provide a useful
basis for discriminating
between one author and another. To test that hypoth-
esis, one could examine
far more examples than I have to determine whether
or not the r
2 values tend to be .889 or higher. The QSUM proponents have
accumulated an enormous amount of this data, and they could easily perform
the necessary calculations. Doing so is necessary to defend the view that
this
"language-habit" is indeed an individual, unconscious habit, and not a
general
fact of language.
For further discussion of the "least-squares regression line" and the
"correlation
coefficient," see David S. Moore, The
Basic Practice of Statistics (New York: W. H. Freeman,
1995),
111–128. One can calculate the value of r in Microsoft Excel by using
the CORREL
function.
I used the following authoritative editions for these works: Volume 3 of The Yale Edition
of the Works of Samuel Johnson,
ed. W. J. Bate and Albrecht B. Strauss (New Haven: Yale Univ.
Press,
1969), 74–79; Jane Eyre: The Clarendon Edition of
the Novels of the Brontës, ed. Jane Jack and
Margaret
Smith (Oxford: Clarendon Press, 1969), 3–6; and To
the Lighthouse: The Definitive Col-
lected Edition of the Novels of
Virginia Woolf (London: Hogarth Press, 1990), 3–6. I did not
count
the abbreviations "Mr." and "Mrs." as two and three letter
words. For the Jane Eyre sample, I
omitted the
four lines of verse on page 4 because I wanted to examine only prose.
|
Alternatives to Cumulative Sums
Studies in bibliography | ||