|
The QSUM Attribution Theory
Studies in bibliography | ||
The QSUM Attribution Theory
The fullest discussion of QSUM appears in Analysing for
Authorship: A Guide
to the Cusum Technique by Jill M. Farringdon
with contributions by A. Q. Morton,
M. G. Farringdon, and M. D. Baker.[3]
This book contains a number of case
studies that argue that: D. H.
Lawrence did not write the short story "The Back
Road" (1913); Muriel Spark's essay "My Conversion" (1961) was partly edited by
journalist W. J. Weatherby; and Henry Fielding was the anonymous translator
of Gustavus Adlerfeld's The Military History of Charles
XII (1740). In a separate
SB article, Jill Farringdon presents additional grounds to
attribute the poem A
Funerall Elegye to John Ford not
William Shakespeare.[4]
Another QSUM analysis
argues that The Dark
Tower, a fantasy novel attributed to C. S. Lewis, was writ-
ten by
more than one author.[5]
The eminent Fielding scholar Martin C. Battestin
strongly endorses
the theory: "I have read [Analysing for Authorship] in
typescript
and can say that here, for the first time, the Cusum technique is
explained in
lucid detail, the objections to it are cogently refuted, and
the theory's efficacy

in a quite literal sense, graphically demonstrated." Battestin's title for his brief
essay cogendy states his belief in the theory's promise: "The Cusum Method:
Escaping the Bog of Subjectivism."[6] The theory's proponents thus apply QSUM
to a range of genres written in a variety of historical periods, and so QSUM has
the potential to be useful to anyone concerned with attribution. It consequently
deserves careful attention.
What are the underlying theoretical principles of QSUM? The proponents
themselves do not know. They believe that certain "language-habits" can distin-
guish the utterance (written or spoken) of one person from another. These
habits
include the frequency of short words (with two, three, or four
letters) and of words
beginning with a vowel. Sometimes short words and
initial-vowel words are used
in combination. Why these particular habits
serve to distinguish one author from
another is unclear. In Analysing for Authorship, Michael Farringdon himself admits
that QSUM "works, but no explanation is yet available. It is too early to
provide
a theoretical scientific reason as to why the technique succeeds"
(241). Perhaps he
hopes that future developments will offer theoretical
support. In the meantime,
one can examine QSUM only in practice, which
Michael Farringdon wholly en-
dorses: "In scientific evidence, what is
required is that an experimental method
be capable of being replicated by
others. When cusum analysis is applied to the
data under examination by
other practitioners and identical results follow, then
the evidence is
verified. That is, utterance by one person will, under analysis,
yield a
consistent graph, and will separate from utterance by other persons. This
is
all that is required scientifically" (241).
In the spirit of this recommendation, I first explain this method using a test
case presented by Jill Farringdon, after which I run other tests. She
chooses a
31-sentence sample of her own writing, included on pages
26–32 of her book.
The sample is entirely by her and therefore the
outcome of any accurate QSUM
analysis should demonstrate that one person
wrote this sample. In the words of
QSUM practitioners, the sample should be
shown to be "homogeneous" or not
a "mixed utterance." Before analyzing the
sample text, one must "process" it
properly. Among other things, she
recommends deleting direct quotations and
removing spaces between the words
of the same proper name and between words

| Sentence # | Words per sentence | Deviation from average | Cumulative sum (qsld) |
| 1 | 12 | −10.258 | −10.258 |
| 2 | 16 | −6.258 | −16.516 |
| 3 | 34 | 11.742 | −4.774 |
| 4 | 7 | −15.258 | −20.032 |
| 5 | 46 | 23.742 | 3.710 |
| 6 | 19 | −3.258 | 0.452 |
| 7 | 4 | −18.258 | −17.806 |
| 8 | 10 | −12.258 | −30.065 |
| 9 | 15 | −7.258 | −37.323 |
| 10 | 18 | −4.258 | −41.581 |
| 11 | 36 | 13.742 | −27.839 |
| 12 | 11 | −11.258 | −39.097 |
| 13 | 22 | −0.258 | −39.355 |
| 14 | 22 | −0.258 | −39.613 |
| 15 | 31 | 8.742 | −30.871 |
| 16 | 33 | 10.742 | −20.129 |
| 17 | 20 | −2.258 | −22.387 |
| 18 | 25 | 2.742 | −19.645 |
| 19 | 32 | 9.742 | −9.903 |
| 20 | 24 | 1.742 | −8.161 |
| 21 | 36 | 13.742 | 5.581 |
| 22 | 22 | −0.258 | 5.323 |
| 23 | 34 | 11.742 | 17.065 |
| 24 | 40 | 17.742 | 34.806 |
| 25 | 15 | −7.258 | 27.548 |
| 26 | 3 | −19.258 | 8.290 |
| 27 | 23 | 0.742 | 9.032 |
| 28 | 20 | −2.258 | 6.774 |
| 29 | 19 | −3.258 | 3.516 |
| 30 | 20 | −2.258 | 1.258 |
| 31 | 21 | −1.258 | 0 |
Total number of words in 31-sentence sample: 690
Average number of words per sentence: 22.258
that represent numerical entities. For the following discussion, I choose her own
sample, which she presumably processed correctly. The first stage involves
count-
ing the number of words in each sentence and then tabulating them.
Then one
determines the average number of words per sentence in the sample.
Then one
determines for each sentence the deviation from this average.
Finally, one calcu-
lates a running total (or cumulative sum, hence the name
of the theory) of these
deviations (abbreviated qsld). Table 1 may help explain this final calculation more
clearly.
The qsld for sentence 1 is −10.258, which is then added to the deviation
for sentence 2 (−6.258) to determine the qsld for sentence 2
(−16.516).
The data in table 1 match Farringdon's data on pages 33 and 55 of her book.
I omit the running total of words per sentence (column 2 on page 55) since that
information is not necessary for any calculation. Also, I have not rounded
off
the cumulative sums to the nearest integer as she suggests on page 19
and shows
in column 5 on page 55. I see no statistical benefit to rounding
to this extent.
Here and elsewhere I have rounded numbers to three decimal
places. While I

self rounds the deviations from averages to three decimal places (column 4 on
page 55).
The second stage of QSUM analysis involves identifying a "language-habit"
that "will remain consistent in the sample of language being tested" (19) and will
distinguish the author of the sample from other possible authors. On pages
20
and 25, Farringdon offers eight possible "language-habits" that could be
tested
by counting the frequency of different kinds of words per
sentence:
- 1. two- and three-letter words
- 2. words starting with a vowel
- 3. two- and three-letter words plus words starting with a vowel
- 4. two-, three-, and four-letter words
- 5. two-, three-, and four-letter words plus words starting with a vowel
- 6. three- and four-letter words
- 7. three- and four-letter words plus words starting with a vowel
- 8. words other than two- or three-letter words
When counting "short" words and words starting with a vowel, one must not
"double-dip" or count the same word twice. (The word "and," for example, is
a three-letter word that begins with a vowel, but it cannot be counted as two
words.) She also states that "the most satisfactory percentage of 'habit'
words per
sentence is between 45 and 55 per cent" (25). For her own writing,
she usually
chooses test #3, two- and three-letter words plus words starting
with a vowel.
For this 31-sentence sample, the average number of these words
per sentence is
11.677, which is 52.5% of the average number of total
words per sentence and is
comfortably within her "satisfactory" range. After
counting the words belonging
to the selected "language-habit" one then
performs cumulative sum calculations
similar to the ones conducted for
sentence length. Table 2 presents these results.
The second column is headed
"23lw+ivw," her abbreviation for "two- and three-
letter words plus words
starting with a vowel." The data in the second column
of table 2 match
Farringdon's data in the last column on page 33. (She does not
provide raw
data for the other two columns, but the resulting graph shows that
my
numbers match hers.)
The third and final stage is to graph the two cumulative sums and to super-
impose the lines to make a "QSUM-chart." If the lines closely correspond, the
sample text is by a single author. If they separate, the sample text results
from a
mixed utterance. Figure 1 is the QSUM-chart for the 31-sentence
sample. The
horizontal axis charts the sequence of sentences in order. The
left vertical axis
charts the cumulative sums of sentence length; the right
vertical axis charts the
cumulative sums of two- and three-letter and
initial-vowel words.
Figure 1 matches figure JMF-3 on page 36 of Farringdon's book. This would
make sense since both figures derive from the same set of data and use the same
method to scale the chart (I discuss scale in more detail later). Thus I
have
replicated the technique correctly. Farringdon comments on this figure:
"What
is here visible in the superimposed QSUM-chart is a consistent habit
running
through a reasonable sample of thirty-one sentences. To the
experienced eye, this
is a homogeneous chart. The two lines track each other
quite smoothly, though
some slight displacement appears around sentences
18–20, resulting in what

| Sentence # | 23lw+ivw | Deviation from average |
Cumulative sum (qs23lw+ivw) |
| 1 | 5 | −6.677 | −6.677 |
| 2 | 12 | 0.323 | −6.355 |
| 3 | 17 | 5.323 | −1.032 |
| 4 | 5 | −6.677 | −7.710 |
| 5 | 25 | 13.323 | 5.613 |
| 6 | 7 | −4.677 | 0.935 |
| 7 | 1 | −10.677 | −9.742 |
| 8 | 4 | −7.677 | −17.419 |
| 9 | 7 | −4.677 | −22.097 |
| 10 | 9 | −2.677 | −24.774 |
| 11 | 21 | 9.323 | −15.452 |
| 12 | 6 | −5.677 | −21.129 |
| 13 | 12 | 0.323 | −20.806 |
| 14 | 11 | −0.677 | −21.484 |
| 15 | 15 | 3.323 | −18.161 |
| 16 | 17 | 5.323 | −12.839 |
| 17 | 13 | 1.323 | −11.516 |
| 18 | 16 | 4.323 | −7.194 |
| 19 | 17 | 5.323 | −1.871 |
| 20 | 15 | 3.323 | 1.452 |
| 21 | 14 | 2.323 | 3.774 |
| 22 | 10 | −1.677 | 2.097 |
| 23 | 19 | 7.323 | 9.419 |
| 24 | 23 | 11.323 | 20.742 |
| 25 | 9 | −2.677 | 18.065 |
| 26 | 2 | −9.677 | 8.387 |
| 27 | 10 | −1.677 | 6.710 |
| 28 | 10 | −1.677 | 5.032 |
| 29 | 8 | −3.677 | 1.355 |
| 30 | 11 | −0.677 | 0.677 |
| 31 | 11 | −0.677 | 0 |
Total number of two- and three-letter and initial-vowel words in 31-sentence sample: 362
Average number of two- and three-letter and initial vowel-words per sentence: 11.677
QSUM-analysts usually call a 'blip': this may be defined as a minor and tem-
porary visual disturbance rather than a continuing separation" (37). Farringdon
explains that the "blip" results from a "high degree of condensed
information"
(37) in sentences 18–20.
I have presented this primer of QSUM for a number of reasons: 1) to show
that I understand the mathematics involved; 2) to show that I can accurately
replicate the method; and 3) to establish a basis upon which I will analyze
further
examples more efficiently. First, though, I want to raise central
questions about
this method.
I can think of a number of objections to the QSUM method. The lack of
any
theoretical justification is troubling, and leaves the skeptical outsider with
no way to challenge the proponents on this basis. I suspect that a linguist
would
be especially dubious, since the "language-habits" used in QSUM do not
cor-
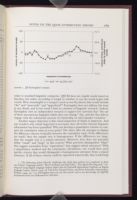

FIGURE 1. Jill Farringdon's sample.
function, but rather according to length or whether or not the words begin with
vowels. How meaningful is a category (such as test #3 above) that would include
"the" and "anaconda" and "apprehend"? Farringdon does not address this issue
in any detail, and in her book I find no citations of linguistic research. Indeed,
Farringdon cites no independent research to support her assertion that "the use
of these unconscious linguistic habits does not change" (84), and she thus fails to
engage with the substantial amount of scholarship on intra-speaker variation.[7]
Another major objection is that visual inspection of charts is imprecise. And
one wonders why visual inspection is necessary since all of the relevant
linguistic
information has been quantified. Why not develop a quantitative
scheme to com-
pare the cumulative sums at every point? The chart, after
all, attempts to display
the difference (shown vertically) between the
cumulative sums. If the differences
are small, then the sample text is
homogeneous. If the differences are large,
then the sample text is a mixed
utterance. However, how does one precisely
define "small" and "large" in
this context? What precisely distinguishes "blips"
that suggest anomalies
from "separations" that suggest mixed utterance? With
a quantitative method
and the consequent calculations, one would then need
specific criteria that
would distinguish a homogeneous utterance from a mixed
utterance. If all of
these criteria could be expressed numerically, that would help


FIGURE 2. Jill Farringdon's sample (modified scale).
used the "chi-squared goodness-of-fit test" which has a sound statistical basis and
is commonly taught in undergraduate statistics courses. It also makes clear what
"small" and "large" mean in specific circumstances. Michael Farringdon refers
to various statistical measures in Analysing for Authorship (though not chi-squared),
but does not delve into them in any significant detail. Furthermore, he concludes
that "I have yet to find these [statistical] measures giving a result that differs
significantly from that found by visual inspection" (261).[8]
Since QSUM relies so much on visual inspection of these charts, one needs
to
recognize a fundamental axiom of charts: scale is important. Changing the
scale changes the chart. For example, figure 2 derives from the same data used
in figure 1, but with different scales for the vertical axes. In figure 2,
the upper
limit is 50 and the lower limit is −50 for both vertical
axes.
Surely, visual inspection of figure 2—whether by the novice or expert QSUM
practitioner—reveals significant separation between these two lines.
Reducing a
scale allows for greater detail to appear, and this is evident in
figure 2. Note the
blank space in the top and bottom quarters of figure 1;
the lines in figure 2 oc-
cupy a greater portion of the space used in the
chart. Note also that the "blips"
Farringdon identified in figure 1 for
sentences 18–20 seem relatively minor com-
pared to the "big blips"
in figure 2 for sentences 12–14. Also, the overlapping
lines in
figure 1 for sentences 6–11 dramatically separate in figure 2. Why would
this be so? Analysing for Authorship is not helpful
here, because Farringdon never
discusses scale using a chart that contains
two lines, and so she does not describe
what happens to a QSUM-chart that
purportedly shows homogeneous author-
ship when one alters the scale even
slightly.

Her brief discussion of scale sets out rules "in order that graphs or charts
may be drawn in a perspective which provides clear information by visual dis-
play" (52). She adds that "the objective is that the graph show the line at
about
one quarter to one third of the vertical range of the sample in
proportion to the
horizontal space" (52). To determine what she defines as
the appropriate scale
for the cumulative sum of sentence length, she first
determines the maximum
and minimum values of this cumulative sum for the
sample chosen. In this in-
stance, the maximum is 34.806 (for sentence 24 in
table 1) and the minimum is
−41.581 (for sentence 10). In this
instance, adding the absolute
values (absolute values ignore the negative
and positive signs) of the maximum and minimum
gives the range, which in
this example is 76.387. Since Farringdon rounds the
cumulative sum for
sentence length to the nearest integer, she finds a range of
77. The
difference is not significant, and so for the purposes of this discussion, I
will treat the range as exactly 77. The scale in figure 1 for the cumulative sum
of sentence length uses 120 as the upper limit and −120 as the lower
limit. The
entire range for this vertical axis is thus 240. If we divide 77
by 240 we get .321,
which is within Farringdon's preference of between one
quarter to one third. In
figure 1, Farringdon's vertical axis on the right
also yields a proportion of .321,
producing almost identical proportions for
the scaling of both vertical axes. The
altered vertical axes in figure 2 use
a range of 100, and the percentages (77/100 =
.77 and 46/100 = .46) are
outside her preference.
Because Farringdon relies solely on a visual impression in relation to the
scale, her method of scaling is arbitrary. (It is also imprecise; "about one
quarter
to one third" allows for enough variation that could significantly
affect the ap-
pearance of the chart.) The arbitrariness of her scaling
method leaves her open
to the charge that she is prejudicial toward the
presentation of her data, as her
method allows her to determine the scale
after performing her calculations. What
she needs
is a scaling method that must be set prior to her
calculations.
To avoid the charge of being arbitrary (and potentially prejudicial), she could
have adopted a standardized scale based on the standard deviation of the
cumu-
lative sums. To create this standardized scale, one would subtract the
mean from
each cumulative sum and divide the difference by the standard
deviation. Figure 3
displays the same data using a standardized scale. This
method requires only
one vertical axis for both lines. This method also
eliminates the arbitrary nature
of her method of scaling. However, the
interpretation of the chart based on a
standardized scale is open to debate.
Does figure 3 reveal that the sample is of
homogeneous or mixed utterance?
The lines overlap for most of the chart, and
the most significant separation
occurs between sentences 17 and 21. Is that sepa-
ration significant? The
separation in figure 3 for those sentences looks greater
than that in figure
1, but it is not clear whether the separation in either figure
is
significant.
So there exists a reliable and consistent way to determine scale that Far-
ringdon could have used. The use of a standardized scale would have removed
any suspicion that she might be manipulating the scale to create charts that skew
her data. However, I cannot determine whether or not she manipulates the
scale
in her book or her recent SB article because
she does not offer the raw data that
provide the basis for her charts. Had
she provided such information she could


FIGURE 3. Jill Farringdon's sample (standardized scale).
the other main objection, namely that the visual inspection of charts invites sub-
jective judgments at odds with QSUM's claims of objectivity.
As serious as these criticisms are, I would like to set them aside for the mo-
ment in order to test QSUM on its own terms. In doing so, I will adhere to
Farringdon's guidelines throughout. The QSUM proponents base the method's
validity almost exclusively on the claim that it "works." But does it?
Cardiff: Univ. of Wales Press, 1996. This book was favorably reviewed by
Peter Smith
in Forensic Linguistics 5 (1998):
77–79, by Kathryn Summers in D. H. Lawrence
Review 28.1–2
(1999): 182–184, and by Warren
Buckland in The Semiotic Review of Books 10.3 (1999):
10–12,
and negatively reviewed by George K. Barr in Expert Evidence 6 (1998): 43–55 and by Pieter
de Haan in Forensic Linguistics 5 (1998):
69–76. For a concise presentation of QSUM, go to the
author's
website at
<http://members.aol.com/qsums/QsumIntroduction.html>.
Kathryn Lindskoog, Sleuthing C. S. Lewis: More Light in
the Shadowlands (Macon, Georgia:
Mercer Univ. Press, 2001),
262–264.
Eighteenth-Century Fiction 8 (1995–96):
533–538. The quotation occurs on page 537.
Battestin's essay is
part of a forum on attribution prompted by J. Paul Hunter's favorable review
of P. N. Furbank and W. R. Owens, Defoe
De-Attributions: A Critique of J. R. Moore's "Checklist"
in Eighteenth-Century Fiction 8
(1995–96): 310–312. Further contributions by Hunter, Isobel
Grundy, Melvyn New, Hugh Amory, Maximillian E. Novak, Carolyn
Woodward, Barbara
Laning Fitzpatrick, and Furbank and Owens appear in
Eighteenth-Century Fiction 8 (1995–96):
519–538; 9 (1996–97): 89–100, 223–225.
Since I cite Battestin here, I want to be clear: QSUM does not play any part in his edition
of New
Essays by Henry Fielding: His Contributions to the Craftsman (1734–1739) and Other Early
Journalism
(Charlottesville: Univ. Press of Virginia, 1989). That volume contains a
"stylometric
analysis" by Michael Farringdon, but this analysis
differs from QSUM, and so my remarks here
do not directly pertain to
the conclusions reached in those attributions, which I have not exam-
ined in any detail. In Analysing for Authorship, Jill
Farringdon promises that "in due course, all
forty-one of the New Essays [attributed to Fielding] will be analysed
by QSUM, and the results
published" (175). I am not aware of any
publication along these lines.
The following article directly challenges the claim that authors are
consistent in their
use of these "language-habits": Pieter de Haan and
Erik Schils, "The Qsum Plot Exposed," Cre-
ating and
Using English Language Corpora: Papers from the Fourteenth International
Conference on English
Language Corpora, Zürich, 1993,
ed. Udo Fries, Gunnel Tottie, and Peter Schneider (Amsterdam:
Rodopi,
1994), 93–105. Farringdon does not cite this article, and to my
knowledge the QSUM
proponents have not addressed its criticisms.
|
The QSUM Attribution Theory
Studies in bibliography | ||